■
Мы округлили полученные значения ![]() и
и ![]() так,
чтобы они были соизмеримы с наблюдаемыми значениями.
так,
чтобы они были соизмеримы с наблюдаемыми значениями.
В математической статистике принято соблюдать два правила округления результатов:
– округлению подвергаются только значения результирующих показателей. Промежуточные значения не округляются;
– конечные значения округляются так, чтобы оставалось на одну (две) значащие цифры больше, чем в первоначальных данных.
Если в выражении, определяющем дисперсию, выполнить следующее преобразование
![]()
то получится другая эквивалентная формула, которая помогает облегчать вычисление дисперсии.
Теорема 2.3 Дисперсия выборки x1, x2, …, xn вычисляется по формуле:
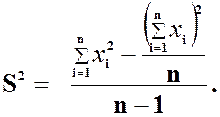
Дисперсия вариационного
ряда x1, x2, …, xn с соответствующими частотами
![]() вычисляется по формуле:
вычисляется по формуле:
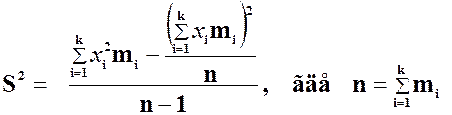 .
.
Дисперсия статистического ряда с соответствующими
интервальными средними ![]() ,
, ![]() , …,
, …, ![]() и
частотами
и
частотами ![]() вычисляется по формуле:
вычисляется по формуле:
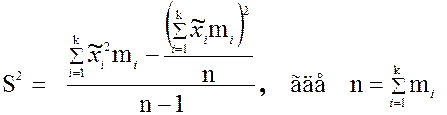 .
.
Заметим, что ни одна из этих формул не требует предварительного
вычисления среднего ![]() . Все данные формулы используются
при малых объемах выборок, при больших объемах делитель n – 1 заменяется на n. Они не только облегчают вычислительную
работу, но и дают более точный результат в тех случаях, когда
при нахождении среднего делаются округления.
. Все данные формулы используются
при малых объемах выборок, при больших объемах делитель n – 1 заменяется на n. Они не только облегчают вычислительную
работу, но и дают более точный результат в тех случаях, когда
при нахождении среднего делаются округления.
Пример 2.25 Вычислим среднее и стандартное отклонение для статистического ряда из примера 1.7 о возрасте пациентов поликлиники. Необходимые расчеты будем записывать в следующей таблице:
Таблица 2.19 – Вычисление среднего и стандартного отклонения возраста пациентов поликлиники.
|
Возраст |
Интервальное среднее |
Частота
|
|
|
|
10–20 20–30 30–40 40–50 50–60 60–70 70–80 80–90 |
15 25 35 45 55 65 75 85 |
17 24 35 48 57 42 21 6 |
255 600 1225 2160 3135 2730 1575 510 |
3825 15000 42875 97200 172425 177450 118125 43350 |
|
250 |
12190 |
670250 |
Используя суммы столбцов, получим:
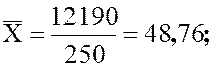
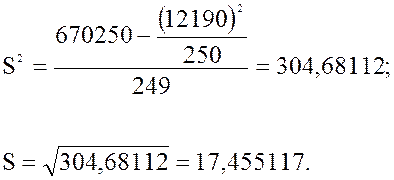
Округлим полученные значения:
![]()
Таким образом, средний возраст пациентов поликлиники равен 48,8 лет, стандартное отклонение равно 17,4 лет.
■
В том случае, когда обследованию подвергается вся генеральная совокупность значений исследуемой случайной величины, то выборочная дисперсия генеральной совокупности совпадает с теоретической дисперсией исследуемой случайной величины Х, которая определяется формулой:
DX = M(X – MX)2.
Далее для обозначения дисперсии генеральной
совокупности мы будем использовать обозначение ![]() 2 =DX,
а стандартное отклонение генеральной совокупности будем обозначать через
2 =DX,
а стандартное отклонение генеральной совокупности будем обозначать через ![]() . Среднее μ и стандартное отклонение
. Среднее μ и стандартное отклонение ![]() генеральной
совокупности в основном используются в теоретической части математической
статистики. Подчеркнем, что выборочное стандартное отклонение S
всегда больше теоретического стандартного отклонения
генеральной
совокупности в основном используются в теоретической части математической
статистики. Подчеркнем, что выборочное стандартное отклонение S
всегда больше теоретического стандартного отклонения ![]() . Однако,
при увеличении объема выборки различие между ними уменьшается.
. Однако,
при увеличении объема выборки различие между ними уменьшается.
Следует отметить, что вместо термина стандартное отклонение часто используются такие названия этого же понятия, как среднее квадратическое отклонение или среднее квадратичное отклонение.
Еще раз подчеркнем, что стандартное отклонение
характеризует степень случайного рассеяния выборочных значений вокруг среднего.
Чем меньше значение S, тем ближе разбросаны выборочные данные вокруг
среднего ![]() . В предельном случае, когда
. В предельном случае, когда ![]() , случайное рассеяние отсутствует, так как
из равенства
, случайное рассеяние отсутствует, так как
из равенства
![]()
следует,
что ![]() , то есть случайная величина является
константой.
, то есть случайная величина является
константой.
Правомерность использования стандартного отклонения s в качестве меры рассеяния конкретных значений случайной величины Х вокруг среднего μ теоретически подтверждается известным неравенством Чебышева:
для любой случайной величины Х, имеющей конечную дисперсию, при каждом ε > 0 справедливо неравенство
Р (│Х – μ │≤ ε) ≥ 1 –![]()
В частном случае, когда ε = ks, где k – целое число большее 1, имеет место следующее неравенство
Р (│Х – μ │ ≤ ks) ≥ 1 – ![]() .
.
Отсюда при k = 2 и k = 3 получаются следствия:
Р (│Х – μ │≤ 2s) ≥ 1 – 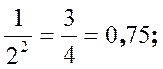 .
.
Р (│Х – μ │≤ 3s) ≥ 1 – 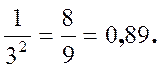
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.