Процентили – это числа, обозначаемые
через ![]() , которые делят исследуемую выборку на 100
равных частей.
, которые делят исследуемую выборку на 100
равных частей.
|
1 % |
1 % |
1 % |
… |
1 % |
1 % |
1 % |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Определение 2.26k-ым
процентилем упорядоченной выборки (0 ![]() 100) называется число
100) называется число ![]() , удовлетворяющее двум условиям:
, удовлетворяющее двум условиям:
1)
в выборке имеется не более
k%
значений, меньших числа ![]() ;
;
2)
в выборке имеется не более
![]() %
значений больших числа
%
значений больших числа ![]() .
.
|
Не более k % |
Не более (100 – k) % |
![]()
Например, если двадцатый процентиль ![]() , то в выборке содержится не более 20 % значений, меньших 14, и не более (100 – 20) % = 80 % значений, больших 14. Очевидно, что 50-й процентиль
, то в выборке содержится не более 20 % значений, меньших 14, и не более (100 – 20) % = 80 % значений, больших 14. Очевидно, что 50-й процентиль ![]() совпадает с медианой выборки:
совпадает с медианой выборки: ![]() Нулевой процентиль
Нулевой процентиль ![]() является наименьшим выборочным значением.
Сотый процентиль
является наименьшим выборочным значением.
Сотый процентиль ![]() равен наибольшему выборочному
значению.
равен наибольшему выборочному
значению.
Более часто используемыми
характеристиками локализации отдельных частей выборки являются так называемые квартили.
Квартили – это числа, обозначаемые через ![]() которые
делят упорядоченную выборку на четыре части:
которые
делят упорядоченную выборку на четыре части:
|
25 % |
25 % |
25 % |
25 % |
![]()
![]()
![]()
Первый квартиль выборки ![]() совпадает
с 25-м процентилем выборки, то есть
совпадает
с 25-м процентилем выборки, то есть ![]() является числом,
большим не более 25 % выборочных значений, и меньшим не более 75 % значений.
является числом,
большим не более 25 % выборочных значений, и меньшим не более 75 % значений.
Второй квартиль ![]() является
медианой. Третий квартиль
является
медианой. Третий квартиль ![]() совпадает с 75-ым
процентилем. Число
совпадает с 75-ым
процентилем. Число ![]() делит выборку на две части:
первая часть, содержащая значения меньшие числа
делит выборку на две части:
первая часть, содержащая значения меньшие числа ![]() , составляет
не более 75 % выборки, вторая часть, содержащая выборочные
значения, большие числа
, составляет
не более 75 % выборки, вторая часть, содержащая выборочные
значения, большие числа![]() , составляет не более 25 % выборки. Итак,
, составляет не более 25 % выборки. Итак, ![]() ,
, ![]() ,
, ![]() .
.
Алгоритм вычисления k-го процентиля
1. Выборка записывается в порядке возрастания выборочных значений от меньшего к большему. Если объем выборки равен n, то после упорядочения каждое выборочное значение занимает определенную позицию или определенный номер от 1 до n.
2. Если k = 50, то процентиль ![]() совпадает с медианой и находится по
алгоритму определения медианы.
совпадает с медианой и находится по
алгоритму определения медианы.
3. При k < 50, вначале вычисляется вспомогательное значение
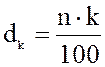 , где n – объем выборки. Если
, где n – объем выборки. Если ![]() получается
дробным числом, то оно округляется до следующего за ним целого числа
получается
дробным числом, то оно округляется до следующего за ним целого числа ![]() . Например, если
. Например, если ![]() ,
то
,
то ![]() . Если
. Если ![]() выражается
целым числом, то берутся два целых числа
выражается
целым числом, то берутся два целых числа ![]() и следующее
за ним
и следующее
за ним ![]() . Например, если
. Например, если 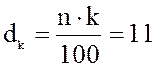 ,
то берутся
,
то берутся ![]() .
.
4. При k > 50 вместо k используется
значение ![]() , которое меньше 50. Затем для
, которое меньше 50. Затем для ![]() выполняются необходимые вычисления из
пункта 3 для нахождения либо одного целого числа
выполняются необходимые вычисления из
пункта 3 для нахождения либо одного целого числа ![]() , либо
двух чисел
, либо
двух чисел ![]() и
и ![]() .
Находится значение процентиля
.
Находится значение процентиля ![]() .
.
5. Если k < 50, то от начала выборки отсчитывается позиция с
номером ![]() . Если
. Если ![]() –
единственное значение, найденное по третьему пункту, то выборочное значение
–
единственное значение, найденное по третьему пункту, то выборочное значение ![]() , стоящее на месте с номером
, стоящее на месте с номером ![]() и будет являться k-ым
процентилем:
и будет являться k-ым
процентилем: ![]() . Если были взяты два значения
. Если были взяты два значения ![]() и
и ![]() , то
находятся два выборочных значения
, то
находятся два выборочных значения ![]() , стоящих на местах с
номерами
, стоящих на местах с
номерами ![]() и
и ![]() .
Процентиль
.
Процентиль ![]() равен полусумме этих значений:
равен полусумме этих значений:
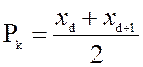 .
.
Если k > 50, то позиция с номером ![]() или
позиции с номерами
или
позиции с номерами ![]() и
и ![]() отсчитываются
от конца выборки. Затем значение
отсчитываются
от конца выборки. Затем значение ![]() находится так же, как
и для k < 50.
находится так же, как
и для k < 50.
По этой схеме вычисляются и квартили.
Пример 2.31 Рассмотрим данные о весе багажа, зарегистрированного пассажирами самолета одного авиарейса.
5,7 10,6 14,8 23,6 29,7 35,5 46,4 56,5
7,4 10,8 15,6 24,4 32,2 36,7 48,1 58,2
8,2 11,7 16,7 25,7 32,6 38,4 49,5 64,8
9,4 12,5 20,4 27,2 33,5 44,3 52,8 68,7
9,8 13,4 22,5 28,5 34,6 45,2 54,7 70,2
По условию ![]() – это объем данной
выборки. Найдем первый квартиль
– это объем данной
выборки. Найдем первый квартиль ![]() , совпадающий с 25-м
процентилем
, совпадающий с 25-м
процентилем ![]() . Итак,
. Итак, ![]() .
Вычислим
.
Вычислим 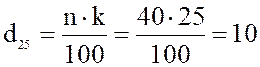 . Получилось целое число, поэтому берем два
значения
. Получилось целое число, поэтому берем два
значения ![]() и
и ![]() .
Находим два выборочных значения, стоящие на 10-м и 11-м местах:
.
Находим два выборочных значения, стоящие на 10-м и 11-м местах: ![]() и
и ![]() , 25-й
процентиль равен их полусумме:
, 25-й
процентиль равен их полусумме: 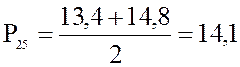 . Итак
. Итак ![]() . Найдем второй квартиль
. Найдем второй квартиль ![]() . Так как
. Так как ![]() – четное число, то находим два
выборочных значения, стоящих на
– четное число, то находим два
выборочных значения, стоящих на ![]() -м месте и на
-м месте и на 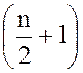 – месте:
– месте: ![]() и x21 = 29,7. Медиана
и x21 = 29,7. Медиана ![]() равна их полусумме:
равна их полусумме: 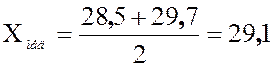 .
Итак,
.
Итак, ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.