Первичная обработка статистических данных. Практическое пособие, страница 25

Определение 2.13 Стандартным отклонением выборки         x₁, x₂, …, x_n называется число S, которое вычисляется по формуле:

.

Таким образом, выборочное стандартное отклонение равно квадратному корню из выборочной дисперсии, следовательно, справедливы формулы:

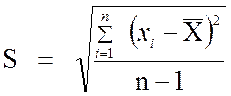либо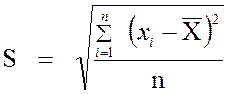   

Пример 2.21  В течение пяти дней студент Ковалев записывал стоимость обедов в студенческой столовой: 3,2; 4,8; 5,6; 4,5; 5,4. Найдем выборочную дисперсию и стандартное отклонение.

Сначала определим среднее:

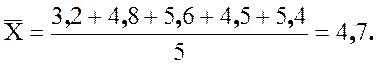
Вычислим дисперсию:

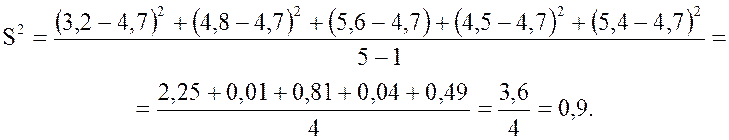
Найдем стандартное отклонение:

Округлим полученное значение:  S = 0,95 условных рублей.

■

Определение 2.14   Выборочной дисперсией вариационного ряда x₁, x₂, …, x_n с соответствующими частотами    называется число  ,  определяемое формулой:

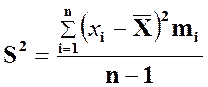     или     

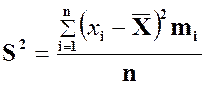
соответственно, при малом и большом значении n,где  .

Пример 2.22 Для социологического исследования были собраны данные о количественном составе 20 семей, приведенные в следующей таблице.

 Таблица 2.16  – Количественный состав семей

Количество членов семьи	1            2            3           4           5          6
	2            3            8           5           1          1

Найдем среднее, дисперсию и стандартное отклонение:

n = 2 + 3 + 8 + 5 + 1 + 1 = 20;

.

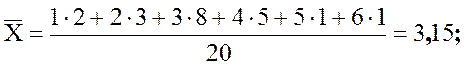
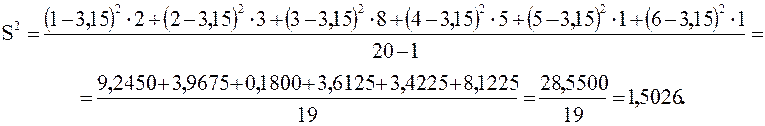
Округлим S² = 1,50 и S = 1,23. Итак,  – это среднее число членов семьи, S = 1,23 – это стандартное отклонение от среднего.

■

Определение 2.15 Выборочной дисперсией статистического ряда, состоящего из  k  интервалов с  соответствующими интервальными средними  и интервальными частотами , называется число  ,  равное:

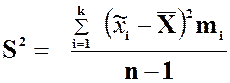     или     ,

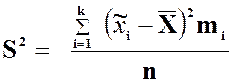соответственно, при малом и большом значении n, где  .

Пример 2.23 Результаты экзамена по высшей математике пятидесяти студентов представлены следующим статистическим рядом. Используется десятибалльная система оценок. Найдем среднее и стандартное отклонение.

 Таблица 2.17 – Итоги экзамена по высшей математике

Оценка	0–2	2–4	4–6	6–8	8–1
	3	9	16	14	8

Итак, 

Найдем интервальные средние:

Вычислим среднее:

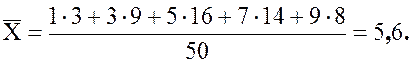
Найдем дисперсию данной выборки:

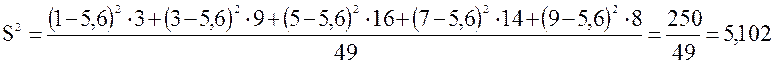Определим значение стандартного отклонения:

.

Итак, средняя оценка студентов I курса составляет 5,6 баллов. Стандартное отклонение  баллов показывает, что оценки большинства студентов отличаются от среднего не более, чем на 2,26 баллов.

■

Таким образом, для вычисления выборочной дисперсии необходимо найти значение среднего , вычислить сумму квадратов отклонений выборочный значений от среднего и разделить ее на   n – 1, где n – число всех наблюдений. Извлечение квадратного корня при нахождении стандартного отклонения возвращает к первоначальному масштабу единицы измерения.

Обработка и анализ статических данных требует кропотливой и нелегкой вычислительной работы. Для организации вычислений в математической статистике часто используются специальные таблицы.

Пример 2.24 Найдем среднее и стандартное отклонение для статистического ряда из примера 1.4 о высоте городских зданий. Все необходимые вычисления будем записывать в таблицу 2.18.

Из таблицы 2.18  берем необходимые промежуточные результаты:

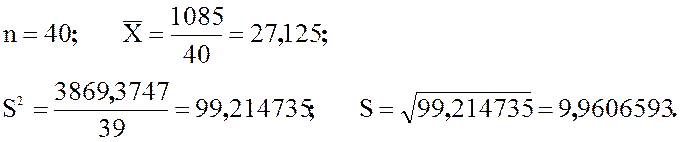
Итак, среднее высоты зданий равно 27,12 метров, а стандартное отклонение  равно 9,96 метров.

Таблица 2.18 – Вычисление среднего и стандартного отклонения высоты зданий