Первичная обработка статистических данных. Практическое пособие, страница 29

2.6 Асимметрия и эксцесс

В математической статистике для выяснения геометрической формы плотности вероятности случайной величины используются две числовые характеристики, связанные с центральными моментами третьего и четвертого порядков.

Определение 2.22   Коэффициентом асимметрии выборки  x₁,  x₂,  …, x_n называется число  ,  равное отношению центрального выборочного момента третьего порядка  к кубу стандартного отклонения  S:

.

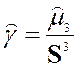Так как   и  ,  то коэффициент асимметрии выражается через центральные моменты следующей формулой:

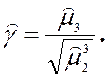
Отсюда получается формула, выражающая коэффициент асимметрии через начальные моменты:

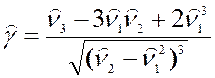, которая облегчает практические вычисления.

Соответствующая  теоретическая  характеристика  вводится   с   помощью  теоретических моментов.

Определение 2.23  Коэффициентом асимметрии случайной величины X называется число  равное отношению центрального момента третьего порядка   к кубу стандартного отклонения  :

.

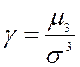Если случайная величина X имеет симметричное распределение относительно математического ожидания  μ, то её теоретический коэффициент асимметрии равен 0, если же распределение вероятностей несимметрично, то коэффициент асимметрии отличен от нуля. Положительное значение коэффициента асимметрии говорит о том, что большая часть значений случайной величины расположена правее математического ожидания, то есть правая ветвь кривой плотности вероятности более удлинена, чем левая. Отрицательное значение коэффициента асимметрии говорит о том, что более длинная часть кривой расположена слева. Данное утверждение иллюстрирует следующий рисунок.

g < 0

g  > 0

                                      

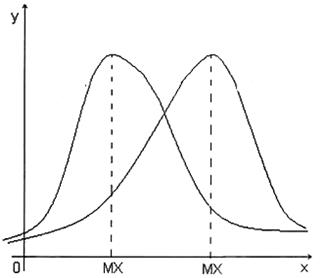
Рисунок 2.1 – Положительная и отрицательная асимметрия

распределений

Пример 2.29 Найдем выборочный коэффициент асимметрии по данным исследования стрессовых ситуаций из примера 2.28.

Пользуясь ранее вычисленными значениями центральных              выборочных моментов, получим

.

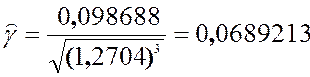Округлим  = 0,07. Найденное отличное от нуля значение коэффициента асимметрии показывает скошенность распределения относительно среднего. Положительное значение   говорит о том, что более длинная ветвь кривой плотности вероятности расположена справа.

■

Особенности распределения значений случайной величины вокруг её модального значения  Х_мод  характеризует следующая постоянная.

Определение 2.24   Эксцессом выборки  x₁,  x₂, …, x_nназывается число  , равное

,

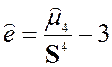где   – выборочный центральный момент четвёртого порядка,

S⁴  – четвёртая степень стандартногоотклонения  S.

Теоретическое понятие эксцесса является аналогом выборочного.

Определение 2.25 Эксцессом случайной величины  X  называется число  е,  равное

,

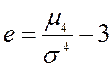где – теоретический центральный момент четвёртого порядка,     

–четвёртая степень стандартного отклонения  .

Значение эксцесса е характеризует относительную крутость вершины кривой плотности распределения вокруг точки максимума. Если эксцесс является положительным числом, то соответствующая кривая распределения имеет более острую вершину. Распределение с отрицательным эксцессом имеет сглаженную и более плоскую вершину. Следующий рисунок иллюстрирует возможные случаи.

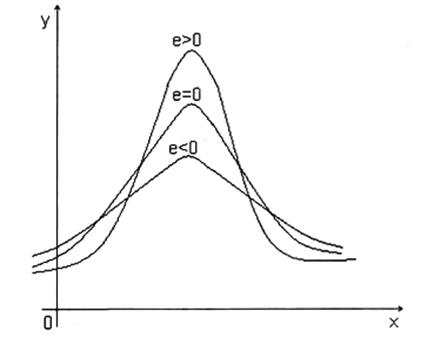
Рисунок 2.2 – Распределения с положительным, нулевым               и  отрицательным значениями эксцессов

Пример 2.30  Вычислим значение выборочного эксцесса по данным исследования стрессовых ситуаций примера 2.28.

Возьмем найденные ранее значения центральных выборочных моментов

 = 5,33745  и   = 1,2704.

Так как   = S²,  то   = S⁴.  Следовательно

.

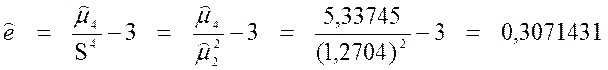После округления   = 0,31 . Положительное значение эксцесса указывает на более острую вершину кривой плотности вероятности.

■

Отметим, что коэффициент асимметрии  и эксцесс  вместе с   и стандартным отклонением  S  являются важными числовыми характеристиками закона распределения исследуемой          величины.

2.7  Процентные точки и квантили распределения

Существуют определенные числовые характеристики, которые описывают месторасположение одной части выборки относительно остальной части упорядоченной выборки. Рассмотрим понятие процентиля, с помощью  которого локализуются позиции наблюдений относительно всей выборки.