|
Рост Х |
Интервальное среднее |
Частота
|
|
|
|
|
150–155 155–160 160–165 165–170 170–175 175–180 |
152,5 157,5 162,5 167,5 172,5 177,5 |
3 12 14 10 7 4 |
-10 -5 0 5 10 15 |
-2 -1 0 1 2 3 |
-6 -12 0 10 14 12 |
|
|
|
Получаем 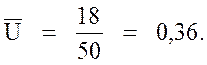
Найдем выборочное среднее по формуле:
![]()
Таким образом, выборочное среднее данной выборки равно 164,3.
■
Заметим, что выборочное среднее несгруппированной выборки в общем виде отличается от выборочного среднего этой выборки, вычисленного после группировки. Однако, для большинства исследований это различие является несущественным.
Формулу для вычисления среднего вариационного ряда можно преобразовать следующим образом:
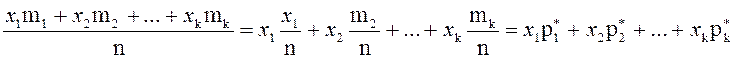 , где
, где ![]() ,
, ![]() , …,
, …, ![]() – относительные частоты соответствующих значений.
Известно что, при неограниченном увеличении числа испытаний
– относительные частоты соответствующих значений.
Известно что, при неограниченном увеличении числа испытаний ![]() относительная частота стремится к
вероятности события:
относительная частота стремится к
вероятности события:
![]() ,
, ![]() , …,
, …,
![]() .
.
Отсюда следует, что
![]() .
.
Таким образом, при увеличении числа испытаний среднее
![]() стремится к математическому ожиданию MX
случайной величины Х, поэтому выборочное среднее
стремится к математическому ожиданию MX
случайной величины Х, поэтому выборочное среднее ![]() является
статистическим аналогом математического ожидания и обладает основными свойствами
математического ожидания. Главное же отличие состоит в том, что математическое
ожидание исследуемой случайной величины является постоянной величиной, а
среднее
является
статистическим аналогом математического ожидания и обладает основными свойствами
математического ожидания. Главное же отличие состоит в том, что математическое
ожидание исследуемой случайной величины является постоянной величиной, а
среднее ![]() является случайной величиной, так как его
значение определяется случайной выборкой. Разные выборки из одной и той же
генеральной совокупности могут иметь разные средние.
является случайной величиной, так как его
значение определяется случайной выборкой. Разные выборки из одной и той же
генеральной совокупности могут иметь разные средние.
Определение 2.5 Число ![]() называется отклонением выборочного
значения xi от среднего
называется отклонением выборочного
значения xi от среднего ![]() .
.
Пример 2.14 Администратор учреждения зафиксировал реальное время, затраченное на обеденный перерыв шестью сотрудниками: 55, 58, 62, 64, 65, 68.
Вычислим среднее:
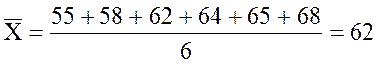 .
.
Найдем отклонения от среднего:
![]()
![]()
![]()
Теперь найдем сумму всех отклонений:
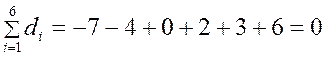 .
.
■
В данном примере сумма всех отклонений от среднего равна 0. Такой результат справедлив и в самом общем случае.
Теорема 2.1 Сумма
всех отклонений выборочных значений x1, x2, …, xn от
их среднего ![]() равна 0.
равна 0.
Это свойство среднего подтверждает его центральную роль в совокупности выборочных данных. Равенство
![]()
показывает,
что выборочные значения окружают среднее ![]() как
справа, так и слева.
как
справа, так и слева.
Интересное свойство среднего связано с суммой квадратов отклонений выборочных значений:
![]()
Теорема 2.2 Если x1, x2, …,
xn –
случайная выборка со средним ![]() , то сумма квадратов разностей
, то сумма квадратов разностей
![]()
принимает свое минимальное значение при ![]() .
.
Например, запишем сумму квадратов разностей для выборки 55, 58, 62, 64, 65, 68 из предыдущего примера:
![]()
Ранее мы нашли среднее данной
выборки ![]() Из тео-ремы 2.2 следует, что эта сумма имеет минимальное значение при
Из тео-ремы 2.2 следует, что эта сумма имеет минимальное значение при ![]() .
.
Выборочная средняя находит более широкое применение, чем другие средние, в практических и теоретических исследованиях. Среднее арифметическое обобщает все значения исследуемой выборки и часто используется в качестве единого представителя всей совокупности выборочных данных. Например, при многократных экспериментальных измерениях некоторой величины за истинное значение часто принимается выборочное среднее. Тем не менее, между средним и каждым индивидуальным выборочным значением существует определенное различие.
2.3 Геометрическое среднее и гармоническое среднее
Существуют определенные генеральные совокупности, для которых больше подходят другие виды средних. Рассмотрим понятия среднего геометрического и среднего гармонического.
Определение 2.6Средним
геометрическим выборки x1, x2, …, xn
с положительными значениями называется число ![]() ,
равное корню n-ой степени из произведения всех элементов выборки:
,
равное корню n-ой степени из произведения всех элементов выборки:
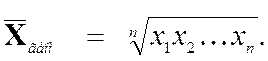
Пример 2.15 Рассмотрим данные о посещаемости студентами группы консультаций по высшей математике. На первой консультации присутствовало 3 студента, на второй – 6, на третьей – 12 студентов.
Итак, выборка состоит из трех значений: 3, 16, 12, n = 3. Вычислим среднее геометрическое по формуле:
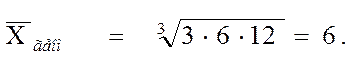
Для сравнения вычислим и среднее арифметическое:
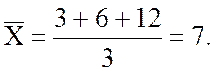
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.