Первичная обработка статистических данных. Практическое пособие, страница 23

Оба эти значения =  6  и   = 7, являясь достаточно близкими, характеризуют среднее число студентов, присутствующих на одной консультации. Заметим, что

.

■

В общем случае выборочное среднее и среднее геометрическое связаны неравенством:

.

Отметим, что формула, определяющая среднее геометрическое, не слишком удобна для расчетов. Поэтому она предпочтительно используется в другом виде:

 

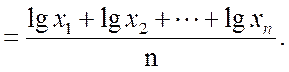
Пример 2.16  Рассмотрим показатели доходности инвестиций финансового фонда в течение пяти последовательных лет:

3,2;   4,5;  7,4;    8,1;   10,5.

Найдем среднее геометрическое  этой выборки:

 

Для вычислений используем логарифмическую формулу:

 

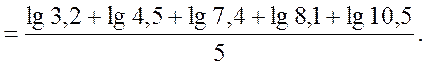
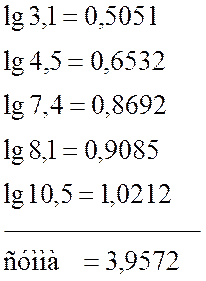
Значит, 

 .

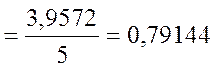Отсюда получаем, что  = 6,14.

Мы получили среднегодовой показатель доходности инвестиций в течение данного пятилетнего периода.

■

Необходимость использования среднего геометрического возникает при исследованиях темпов изменения величин, когда результаты последующих измерений пропорционально зависят от ранее достигнутых значений. Среднее геометрическое дает более точную характеристику  центра выборки и в том случае, когда она состоит из ряда достаточно отдаленных друг от друга значений.

Решим следующую простую задачу.

Автомобиль половину пути проехал со скоростью   км/час, а вторую половину – со скоростью  км/час. Какой была средняя скорость автомобиля на этом пути?

Обозначим через  расстояние, равное половине пути.                Тогда время, затраченное на первую половину пути равно 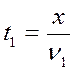     , а на вторую – 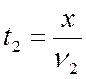. Время всего движения составляет  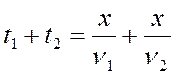. Значит, средняя скорость на всем пути равна:

.

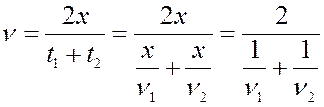Итак, средняя скорость движения определяется выражением:

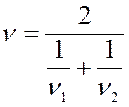
В общем случае для подобных задач существует понятие среднего гармонического.

Определение 2.7 Средним гармоническим выборки x₁, x₂, …, x_n называется число   ,  которое вычисляется по формуле:

 .

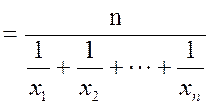Другими словами, среднее гармоническое получается делением объема выборки n на сумму обратных чисел для выборочных         значений.

Пример 2.17  За один час работы на компьютере первый студент набрал 2 страницы текста, второй – 3 станицы, третий – 6, четвертый – 12. Найдем среднее гармоническое числа страниц, которые может набрать на компьютере за один час студент этой группы.

Мы имеем выборку из четырех наблюдений:

2,   3,   16,   12.

Вычислим среднее гармоническое:

 

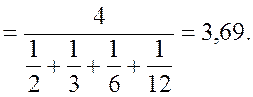
Следовательно, можно предполагать, что в среднем студент этой группы может набрать 3,69 станицы за один час.

■

Определение 2.8 Средним гармоническим вариационного рядаx₁,  x₂, …, x_nс соответствующими частотами   называется число  ,  которое вычисляется по формуле:

.

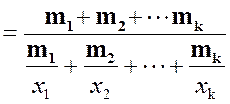Пример 2.18 На решение одной задачи два студента тратят по 10 минут, 3 студента – по 20 минут, 5 студентов – по 30 минут,       4 студента – по 40 минут. Найдем среднее гармоническое времени, необходимого на решение одной задачи.

По данным задачи составим вариационный ряд.

Таблица 2.15 – Затраты времени студентов на решение задачи

Время	10	20	30	40
	2	3	5	4

Вычислим среднее гармоническое:

.

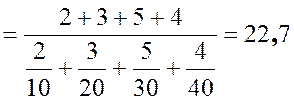Итак среднее гармоническое времени, необходимого для решения одной задачи для этой группы студентов составляет 22,7 минут.

Мы видим, что  = 22,7   меньше   = 27,8.

■

Подчеркнем, что во всех случаях среднее гармоническое, среднее геометрическое и среднее арифметическое удовлетворяют        неравенству:

.

Понятие среднего гармонического используется при исследовании некоторых физических, химических, биологических явлений, а также в экономике.

Мы рассмотрели несколько разных понятий выборочных характеристик среднего. Поэтому применение любого из них необходимо сопровождать дополнительным пояснением.

2.4  Выборочная дисперсия и стандартное отклонение

Выборочное среднее является важной, но не достаточной числовой характеристикой распределения исследуемой случайной величины. Любая случайная выборка состоит из индивидуальных значений, которые могут существенно отличаться и друг от друга, и от среднего. Некоторые значения могут располагаться близко к центру, а другие могут быть значительно отдалены от него. Очевидно, что экспериментальные выборочные значения характеризуются определенной степенью рассеяния вокруг среднего.