Первичная обработка статистических данных. Практическое пособие, страница 12

[5;10), [10;15), [15;20), [20;25), [25;30), [30;35), [35;40), [40;45), [45;50].

Теперь считаем частоту выборочных значений для каждого интервала:

; ; ; ; ; ; ; ; .

Проверка подтверждает правильность равенства

.

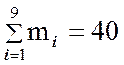Далее вычисляем относительные частоты:

;  ; ; ;

; ; ; ; .

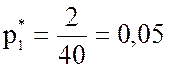Суммирование относительных частот показывает, что равенство 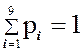   выполняется. Запишем статистический ряд.

Таблица 1.7 – Статистический ряд измерений высоты зданий

Высота зданий	5–10	10–15	15–20	20–25	25–30	30–35	35–40	40–45	45–50
	2	3	5	6	8	7	5	3	1
	0,050	0,075	0,125	0,150	0,200	0,175	0,125	0,075	0,025

■

Вместо короткого названия статистический ряд часто используются более точные по смыслу такие названия, как статистическое распределение выборки, или статистический закон распределения.

Напомним, что в теории вероятностей законом распределения дискретной случайной величины называется соответствие между всеми её возможными значениями и их вероятностями. Статистическое распределение отличается от теоретического вероятностного распределения тем, что вероятность отдельных значений в математической статистике заменяется их относительной частотой.

1.7 Графическое представление статистических данных

Существуют разные графические способы представления статистических распределений выборок или статистических рядов. Любое наглядное изображение статистических данных способствует лучшему пониманию их общих закономерностей.

Вначале рассмотрим традиционный способ графического изображения вариационного ряда. Для этого возьмем прямоугольную систему координат. По определению вариационный ряд состоит из пар чисел вида:

, , … , , где значения x_i являются вариантами выборки, а  являются соответствующими частотами, i = 1, 2, ... , k. В данной системе координат отмечаем k точек с соответствующими координатами:

, , … , , и соединяем их последовательно отрезками прямых.

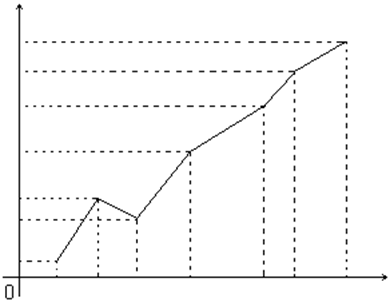
Определение 1.17  Полигоном частот вариационного ряда называется ломаная линия, состоящая из отрезков прямых, последовательно соединяющих точки с координатами (x_i; m_i) , где x_i  пробегает все варианты выборки, а m_i– их соответствующие частоты,  i = 1,2, …,k .

                                 

   

       

                                х

Рисунок 1.7 – Полигон частот вариационного ряда

Пример 1.9  Построим полигон частот для вариационного ряда из примера 1.6, представляющего результаты исследования посещаемости библиотеки  студентами.

Для этого мы отмечаем точки  (0;5),  (1;6),  (2;7),  (3;2),  (4;3),  (5;2)  и последовательно соединяем их.

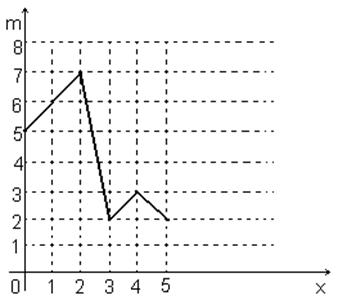
Рисунок 1.8 – Полигон частот данных

посещаемости библиотеки студентами

■

Если частоты вариант заменить соответствующими относительными частотами, то получится  полигон относительных частот.

Определение 1.18  Полигоном относительных частот вариационного ряда называется ломаная линия, состоящая                         из отрезков прямых, последовательно соединяющих точки с координатами где  пробегает все варианты выборки, а – их соответствующие относительные частоты,                i = 1, 2, … , k .

Пример 1.10  Построим полигон относительных частот для вариационного ряда примера 1.6.

Для этого в системе координат отмечаем точки  (0; 0,20), (1; 0,24), (2; 0,28),  (3; 0,08), (4; 0,12), (5; 0,08) и соединяем их последовательно.

y

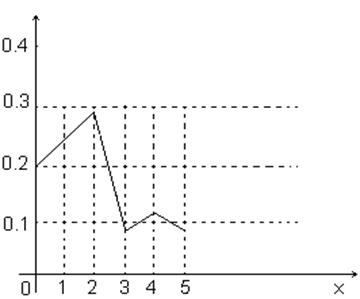
Рисунок 1.9 – Полигон относительных частот данных

посещаемости библиотеки студентами

■

Интервальный статистический ряд удобно представлять графически в виде плоской ступенчатой диаграммы, которая называется гистограммой.

Гистограмма частот статистического ряда строится следующим образом. В прямоугольной системе координат на оси абсцисс отмечаются интервалы данного статистического ряда. Затем на каждом интервале, как на основании, рисуется прямоугольник, высота которого равна частоте этого интервала.