Первичная обработка статистических данных. Практическое пособие, страница 8

Определение 1.10 Функцией распределения случайной величины Х называется функция F_x(x) действительной переменной  х Î (-¥; ¥), равная вероятности того, что Х принимает значения, меньшие числа х.

Таким образом, функция распределения случайной величины Х определяется следующим соотношением:

F_x(x) = P(X < x),  x Î(-¥; ¥).

В дальнейшем вероятностную функцию распределения F_x(x) мы будем называть теоретической. Иногда вместо термина «функция распределения» используется равнозначный термин «интегральная функция распределения».

Пример 1.5 Обозначим через Х число нечетных цифр в произвольном четырехзначном номере. Найдем функцию распределения случайной величины Х и построим ее график.

Очевидно, что случайная величина Х может принимать следующие значения: 0, 1, 2, 3, 4.

Вероятность выбора одной нечетной цифры равна 0,5, вероятность выбора четной цифры также равна 0,5. Вычислим вероятности соответствующих значений. р₀ = Р(Х = 0) = С₄⁰ (0,5)⁰ (0,5)⁴ = 0,0625

р₁ = Р(Х = 1) = С₄¹ (0,5)¹ (0,5)³ = 0,2500

р₂ = Р(Х = 2) = С₄² (0,5)² (0,5)² = 0,3750

р₃ = Р(Х = 3) = С₄³ (0,5)³ (0,5)¹ = 0,2500

р₄ = Р(Х= 4) = С₄⁴ (0,5)⁴ (0,5)⁰ = 0,0625

Суммирование вероятностей подтверждает условие нормированности распределения.

Пусть  xÎ (-¥; 0],  тогда

F_x(x) = P(X < x) = P(X < 0) = 0.

При  x Î (0; 1]  имеем

F_x(x) = P(X < x) = P(X < 1) = Р(X = 0) = 0,0625.

При  x Î (1; 2]  имеем

F_x(x) = P(X < x) = P(X < 2) = P(X = 0) + Р(Х = 1) =

= 0,0625 + 0,2500 = 0,3125.

При  x Î (2; 3]  имеем

F_x(x) =Р(X < x) = P(X < 3) = P(X = 0) + Р(Х = 1) + Р(Х = 2) = 0,0687.

При  x Î (3; 4]  имеем

F_x(x) = P(X < x) = P(X < 4) =

= P(X = 0) + Р(Х = 1) + Р(Х = 2) + Р(Х =3) = 0,9375.

Наконец, при  x  (4; )  имеем

F_x(x) = P(X < x) =

= P(X = 0) + Р(Х = 1) + Р(Х = 2) + Р(Х = 3) + Р(Х = 4) = 1.

В итоге получается следующее выражение функции распределения:

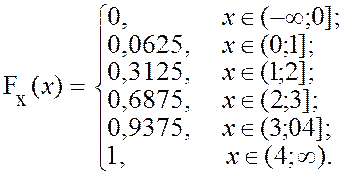
Построим график этой функции.

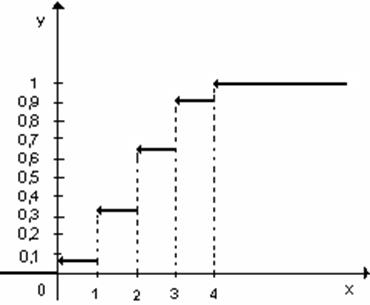
Рисунок 1.2  – График функции распределения числа

четных цифр в произвольном четырехзначном номере

■

В общем случае функция распределения любой дискретной случайной величины Х находится по формуле:

F_x(x) = Σ  P (X = x_i),

x_i < x

то есть суммируются вероятности всех значений случайной           величины, которые являются меньшими числа х.

Напомним основные свойства функции распределения.

1. Функция распределения является неубывающей функцией, то есть

F_x  (x₁)  ≤  F_x(x₂)  при  x₁ < x₂.

2. Справедливы следующие равенства:

lim F_x(x) = 0   и   lim F_x(x) = 1.

x→ - ¥                         x→ + ¥

3.  Все значения функции распределения изменяются от             0 до 1, то есть

0 ≤  F_x(x) ≤ 1.

4.  Функция распределения является непрерывной слева, то есть

lim F_x(x) =  F_x(x₀).

x → x₀ – 0        

5. Вероятность  неравенства   a ≤ X < b для любых  а  и  b вычисляется по формуле

P (a ≤ X < b) = F_x(b) – F_x(a).

Подчеркнем, что функция распределения является наиболее общей формой закона распределения и самой полной характеристикой случайной величины любого типа.

1.5 Плотность распределения вероятностей

Результаты не всех реальных экспериментов можно исчерпывающе описать с помощью дискретных случайных величин. Например, основные метеорологические параметры погоды и физиологические показатели состояния здоровья человека такие, как температура, давление, вес, размеры, промежутки времени, концентрация химических веществ в жидкости изменяются              непрерывно от наименьшего возможного значения до наибольшего. Если множество возможных значений случайной величины заполняют некоторый конечный или бесконечный числовой интервал, то такая случайная величина называется непрерывной.

Подчеркнем, что непрерывная случайная величина в отличие от дискретной имеет бесконечное множество значений, которые невозможно перечислить. Из определения непрерывности  вытекает и другая ее особенность.

Вероятность любого конкретного значения х непрерывной случайной величины Х равна нулю, то есть

P(Х = х) = 0.