Первичная обработка статистических данных. Практическое пособие, страница 10

у = px(x)

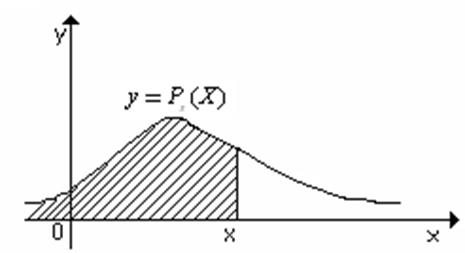
Рисунок 1.6 – Геометрическая интерпретация

функции распределения F_х(х)

Подчеркнем, что функция распределения и плотность вероятности случайной величины являются фундаментальными понятиями как теории вероятности, так и математической статистики. Заданные в аналитической форме, они дают существенную информацию об исследуемой случайной величине и позволяют теоретически обосновать статистические выводы, сделанные на основе эмпирических данных.

1.6 Группировка статистических данных

Полученные в результате экспериментов или наблюдений первичные статистические данные, как правило, записываются в рабочую таблицу наблюдений. К сожалению, на основе неорганизованного скопления числовых значений сложно сделать какие-либо статистические выводы. Прежде всего необходимо представить результаты экспериментов в рабочем виде. Существуют определенные способы группировки статистических данных в специальные таблицы.

Допустим, что в результате проведения nэкспериментов             получена некоторая выборка значений случайной величины Х. Расположим данные выборочные значения в порядке их возрастания, при этом некоторые из них могут повторяться несколько раз.

Определение 1.12 Все различные значения случайной величины, содержащиеся в выборке, называются вариантами.

Определение 1.13 Число m_i, показывающее, сколько раз варианта x_i встречается в выборке, называется частотой варианты  x_i.

Очевидно, что если 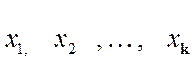 –  все варианты выборки, то сумма их соответствующих частот равна объему всей выборки:

.

Определение 1.14 Если объем всей выборки  равен n, то относительной частотой варианты x_i называется число  , равное отношению частоты   m_i   к объему   n:

.

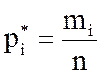Каждая варианта выборки 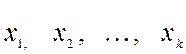 имеет соответствующую относительную частоту:

.

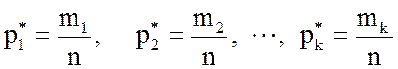Не трудно проверить, что сумма относительных частот всех вариант выборки равна 1:

.

Определение 1.15Множество всех вариант выборки, расположенных в порядке возрастания их значений, вместе с их соответствующими частотами или относительными частотами называется вариационным рядом.

Вариационный ряд удобно представлять в виде следующей таблицы.

Таблица 1.3 – Вариационный ряд

	…
	…
	…

Пример 1.6 В течение недели было проведено исследование посещаемости университетской библиотеки студентами группы, состоящей из 25 человек. Зафиксированное число посещений каждого студента представляет  следующая выборка:

2     2     1     2     2

0     5     0     2     0

1     0     4     1     1

4     2     1     0     2

3     3     4     5     1

Объем выборки  n = 25. Выпишем все варианты в порядке их возрастания:

0,  1,  2,  3,  4,  5.

Найдем частоту каждой варианты:

.

Для проверки найдем сумму всех частот:

5 + 6 + 7 + 2 + 3 + 2 = 25.

Теперь вычислим относительные частоты соответствующих вариант:

;   ;   ;

;    ;    .

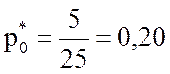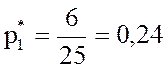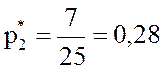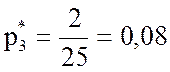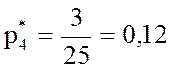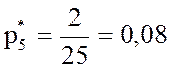Проверим сумму:

0,20 + 0,24 + 0,28 + 0,08 + 0,12 + 0,08 = 1.

Составим вариационный ряд данной выборки.

Таблица 1.4 – Вариационный ряд данных посещаемости библиотеки

■

Вариационный ряд  часто помогает сгруппировать и более организованно записать результаты статистических экспериментов. Однако преимущества вариационного ряда теряются в тех случаях, когда выборка имеет большой объем и не содержит повторяющихся значений. Для выборочных данных  с большим объемом существует более общая форма представления.

Рассмотрим произвольную выборку значений случайной величины Х объема n. Обозначим через  а  наименьшее выборочное значение, а через b – наибольшее. Тогда вся выборка принадлежит отрезку [а; b]. Разделим этот отрезок  точками на  k  меньших интервалов равной длины: