Первичная обработка статистических данных. Практическое пособие, страница 15

Высота зданий	5–10	10–15	15–20	20–25	25–30	30–35	35–40	40–45	45–50
	2	3	5	6	8	7	5	3	1
	0,050	0,075	0,125	0,150	0,200	0,175	0,125	0,075	0,025

Объём исследуемой выборки  n = 40. Вычислим значения эмпирической функции распределения на границах интервалов.

;  ;  ;

;  ;

;  ;  ;

 ;  .

y

По соответствующим точкам (5;0), (10; 0,050), (15; 0,125), (20; 0,250), (25, 0,400), (30; 0,600), (35; 0,775), (40; 0,920), (45; 0,975), (50;1) построим приближенный график эмпирической функции распределения.

x

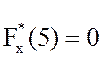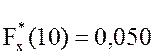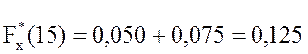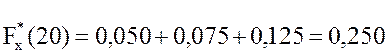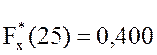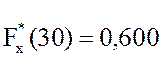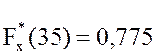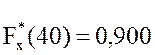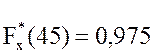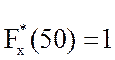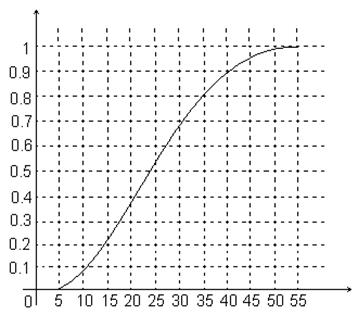
Рисунок 1.14 – График эмпирической функции распределения

высот зданий  города

■

Эмпирическая функция распределения обладает всеми свойствами теоретической функции распределения.

1. Эмпирическая функция распределения является неубывающей функцией, то есть 

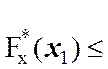
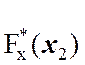 приx₁  < x₂ .

2.  Справедливы следующие равенства:

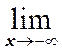
   и .

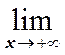
 3. Все значения эмпирической функции распределения       находятся между 0 и 1, то есть

0   1,

4. Эмпирическая функция распределения является непрерывной слева, то есть

=.

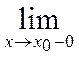
Подчеркнем, что эмпирическая функция распределения является статистическим аналогом теоретической функции распределения. Она помогает приближенно оценить общий характер закона распределения исследуемой случайной величины. Однако необходимо понимать, что на любом эмпирическом распределении отражается влияние многих случайных факторов.

Упражнения   

1.1   Группа студентов, состоящая из 25 человек, должна выбрать 5 делегатов для участия в студенческой профсоюзной конференции. Было проведено голосование и выбрано 5 студентов, получивших большинство голосов. Можно ли считать такой выбор случайным? Обоснуйте свой ответ.

1.2   В библиотеке имеется только 15 задачников и 20 учебников по высшей математике на группу, состоящую из 28 студентов. Опишите процедуру справедливого на ваш взгляд распределения книг.

1.3   На 500 первокурсников, нуждающихся в общежитии, выделено только 70 мест. Распределите места в общежитие с помощью таблицы случайных чисел.

1.4   На участие в телешоу поступило 2700 заявок от зрителей. Для первого тура необходимо выбрать 50 участников. Сделайте справедливый выбор с помощью таблицы случайных чисел.

1.5   Коллектив предприятия состоит из 240 мужчин и 80 женщин. Для анкетирования нужно выбрать 10 % работников предприятия так, чтобы отношение 3:1 мужчин и женщин сохранилось. Составьте список анкетируемых.

1.6   При регистрации кандидат в депутаты представил 10000 подписных листов. Избирательная комиссия должна проверить не         менее 1000 из представленных листов. Каким образом провести случайный отбор проверяемых листов с помощью таблицы случайных чисел?

1.7   Опишите возможную процедуру выбора 12 присяжных        заседателей для суда.

1.8   По данным о числе отсутствующих на занятиях студентов, собранных в течение 25 дней, составьте вариационный ряд и постройте полигон частот и полигон относительных частот.

4	2	3	5	4
2	0	1	3	2
2	1	0	1	1
1	1	2	2	2
3	4	3	2	3

1.9  Составьте вариационный ряд и постройте полигон относительных частот по данным экзаменационным оценкам студентов  1 курса. Найдите эмпирическую функцию распределения оценок.