Первичная обработка статистических данных. Практическое пособие, страница 21

Вычислим интервальные средние всех интервалов:

                    

                                 

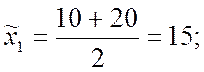
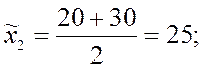
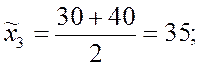
Найдем выборочное среднее:

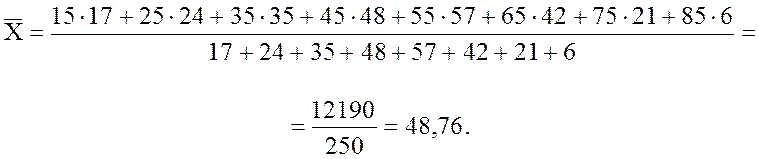
Среднее    характеризует средний возраст наиболее нуждающихся в лечении пациентов.

■

Пример 2.11 Найдем выборочное среднее для статистического ряда из примера 1.8. по данным о высоте зданий:

Таблица 2.10 – Данные исследования высоты зданий

Высота зданий	5–10 7,5	10–15 12,5	15–20 17,5	20–25 22,5	25–30 27,5	30–35 32,5	35–40 35,4	40–45 42,5	45–50 47,5
	2	3	5	6	8	7	5	3	1

Объем исследуемой выборки  . Вычислим интервальные средние:

       

                     

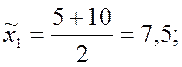
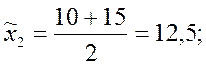
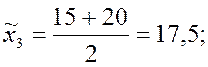
Найдем выборочное среднее:

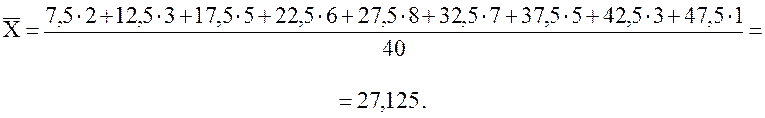
Итак,   метров – это среднее  высот зданий данной выборки.

■

Существуют различные приемы, облегчающие вычислительную работу при нахождении выборочного среднего.

Если выборка содержит большие числа или многократно повторяющиеся близкие значения, то статистические данные можно преобразовать с помощью следующего равенства:

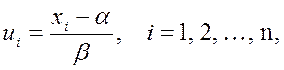
где    и   –  любые действительные числа, причем  .

Число  подбирается так, чтобы разности  были бы наименьшими, число    изменяет масштаб данных.

В результате преобразования данная выборка  x₁,  x₂,  …,  x_n заменяется выборкой    с такими же соответствующими частотами.

Выборочная средняя  выражается через выборочную среднюю  по формуле:

.

Правильный подбор значений  и   обычно облегчает нахождение среднего.

Отметим, что при вычислении выборочных числовых показателей удобно пользоваться определенными расчетными таблицами, в которые обычно записывают необходимые промежуточные  результаты.

Пример 2.12 Найдем среднее возраста пациентов поликлиники по статистическому ряду из примера 1.3., используя преобразования выборочных данных.

Таблица 2.11 – Данные исследования возраста пациентов                поликлиники

Положим, что  . Такой выбор обусловлен тем, что именно это значение имеет наибольшую частоту. В качестве    выберем длину интервалов, то есть  .

Запишем формулу преобразования выборки:

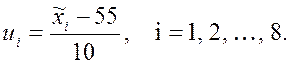
Все необходимые расчеты будем записывать в следующей таблице.

Таблица 2.12 – Вычисления среднего возраста пациентов                поликлиники

Найдем  .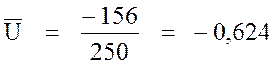

Выборочное среднее    вычислим по следующей формуле:

Это значение    совпадает  с  ранее  найденным  значением из примера 2.10.

■

Пример 2.13 Следующий статистический ряд представляет       результаты проведенного измерения роста пятидесяти семнадцатилетних девушек.

Таблица  2.13 – Данные измерения роста

Для вычисления среднего, прежде всего найдем интервальные средние:

   

      

В качестве  выберем интервальное среднее с наибольшей частотой: . Положим  ,  что совпадает с длиной интервалов.

Преобразуем данные по формуле:

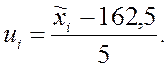
Дальнейшие вычисления записываем в следующей таблице:

Таблица 2.14 – Вычисление среднего роста девушек