Первичная обработка статистических данных. Практическое пособие, страница 7

Таблица 1.1 – Распределение вероятностей числа попаданий         в мишень

■

Определение 1.9 Совокупность всех возможных значений дискретной случайной величины Х и соответствующих им вероятностей  называется законом распределения вероятностей случайной величины.

Более кратко закон распределения вероятностей называют просто распределением случайной величины Х. Часто распределение вероятностей задается таблицей, содержащей все возможные значения случайной величины Х и соответствующие           вероятности этих значений.

Таблица 1.2 – Закон распределения вероятностей случайной дискретной величины Х

Очевидно, что сумма вероятностей всех возможных значений дискретной случайной величины Х равна 1:

р₁ + р₂ + … + р_n + … = 1.

Это свойство называется условием нормированности распределения.

Однако более удобно закон распределения вероятностей дискретной случайной величины выражать некоторой функцией, позволяющей найти вероятность реализации каждого конкретного значения случайной величины Х.

Пример 1.3 Монета бросается семь раз. Обозначим через Х число появлений герба. Найдем закон распределения случайной величины Х.

Очевидно, что случайная величина Х может принимать следующие значения: 0, 1, 2, 3, 4, 5, 6, 7. При этом вероятность того, что значение переменной Х равно k вычисляется по формуле  Бернулли:

P(Х = k) = P₇(k) = С₇^k(0,5)^k(0,5)^7-k, где k = 0, 1, 2, 3, 4, 5, 6, 7. Данная функция полностью определяет распределение вероятностей случайной величины Х.   

■

В некоторых случаях используется графическое изображение закона распределения вероятностей случайной величины. Для этого на оси абсцисс отмечаются все значения случайной величины х₁, х₂, …, х_n, а на оси ординат откладываются соответствующие вероятности р₁, р₂, …, р_n. Затем точки с координатами (х₁; р₁), (х₂; р₂), …, (х_n; р_n) последовательно соединяются отрезками. Полученная ломаная линия называется многоугольником распределения вероятностей.

Графическое изображение закона распределения позволяет получить визуальное представление об исследуемой зависимости. С помощью графика можно заметить основные тенденции варьирования значений случайной величины. Особенно полезны графики в тех случаях, когда нужно показать постоянство некоторых          характеристик закона распределения.

Пример 1.4  Построим многоугольник распределения вероятностей для случайной величины Х по данным предыдущего примера 1.3.

Прежде всего, вычислим вероятность каждого возможного        значения:

р₀ = Р(Х = 0) = С₇⁰ (0,5)⁰ (0,5)⁷ = 0,0078125

р₁= Р(Х = 1) = С₇¹ (0,5)¹ (0,5)⁶ = 0,0546875

р₂ = Р(Х= 2) = С₇² (0,5)² (0,5)⁵ = 0,1640625

р₃ = Р(Х= 3) = С₇³ (0,5)³ (0,5)⁴ = 0,2734375

р₄ = Р(Х = 4) = С₇⁴ (0,5)⁴ (0,5)³ = 0,2734375

р₅ = Р(Х = 5) = С₇⁵ (0,5)⁵ (0,5)² = 0,1640625

р₆ = Р(Х = 6) = С₇⁶ (0,5)⁶ (0,5)¹ = 0,0546875

р₇ = Р(Х = 7) = С₇⁷ (0,5)⁷ (0,5)⁰ = 0,0078125

Проверка показывает, что сумма вероятностей всех значений равна 1.

Округлим значения вероятностей:

Выполним построение многоугольника распределения вероятностей.     

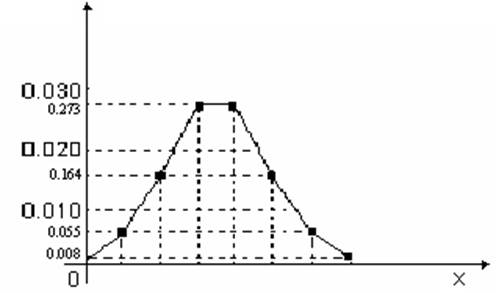
Рисунок 1.1 – Многоугольник распределения вероятностей

для числа появления герба при семикратном бросании монеты

■

1.4 Функция распределения случайной величины

Все рассмотренные способы задания закона распределения случайной величины являются неприемлемыми тогда, когда случайная величина имеет слишком много значений, которые невозможно перечислить. Для исследования закона распределения вероятностей произвольной случайной величины Х можно использовать не вероятность события Х = х, а вероятность события           Х < х, где  х – некоторое действительное число. Вероятность того, что случайная величина Х в результате опыта примет значение, которое будет меньше числа  х, является функцией аргумента х.