Первичная обработка статистических данных. Практическое пособие, страница 20

■

Заметим, что медиана существует в любой статистической выборке. Следует подчеркнуть и такое полезное свойство медианы как её нечувствительность  к месторасположению экстремальных значений в больших выборках. Наличие в выборке сильно отклоняющихся значений создает определенные проблемы при анализе, поэтому использование медианы позволяет в определенных случаях обойти некоторые трудности.

Известно, что существуют симметричные и асимметричные распределения случайных величин. В том случае, когда выборочные данные реализуют симметричное распределение, то значение медианы и моды практически совпадают. Для асимметричных распределений равенство не выполняется.

2.2 Выборочное среднее

Теперь рассмотрим наиболее часто используемое понятие среднего, которое в отличие от моды и медианы объединяет все выборочные значения.

Определение 2.3 Средним арифметическим выборки x₁, x₂, …, x_n значений случайной величины  Х  называется число ,  равное сумме всех выборочных значений, деленной на число всех наблюдений  n:

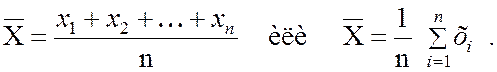
Обычно среднее арифметическое  называется выборочным средним или просто средним.

В случае, когда выборка совпадает со всей исследуемой генеральной совокупностью, то таким же образом вычисляется её генеральное среднее. В дальнейшем выборочное среднее всей генеральной совокупности значений случайной величины Х будем обозначать символами  или  и называть генеральным средним.

Пример 2.7  Студент Денисов по пяти предметам получил  следующие экзаменационные оценки по десятибальной системе:              8,   9,   8,  7,   6. Вычислим среднее данных оценок:

.

■

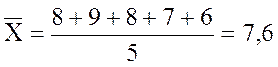Подчеркнем, что выборочное среднее не обязательно должно быть элементом самой выборки. В том случае, когда выборка представляется вариационным рядом, содержащим    вариант  x₁, x₂, …, x_k с соответствующими частотами  ,  то среднее  вычисляется по следующей формуле:

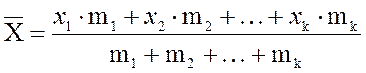,    или

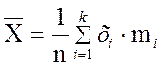       ,  где  .

Пример 2.8 Результаты экзамена по математике для группы студентов, состоящей из 25 человек, представлены следующим вариационным рядом:

Таблица 2.7  – Экзаменационные оценки группы студентов

Найдем среднее:

■

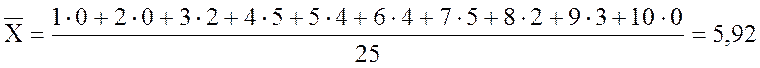
Пример 2.9 Для вариационного ряда данных о посещаемости университетской библиотеки из примера 1.6., найдем среднее, моду и медиану:

  Таблица 2.8 – Вариационный ряд данных  посещаемости           библиотеки

Вычислим среднее:

.

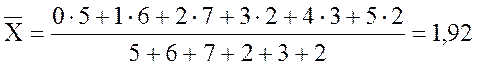Очевидно, что мода данного ряда . Легко находится и медиана . Среднее  меньше моды и медианы, равным 2. Равенство  приводит к предположению о симметричности этого распределения.

■

В случае, когда выборка сгруппирована в виде статистического ряда, состоящего из k интервалов

,  , …,  ,  …,  , то конкретные выборочные значения могут быть неизвестными, и рассмотренные выше формулы не пригодны для вычисления среднего. Поэтому для каждого интервала вычисляется  его середина, или интервальное среднее по формуле:

.

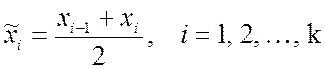При выполнении вычислений каждое выборочное значение, принадлежащее интервалу, заменяется интервальным средним.

Определение 2.4 Если   – интервальные средние, а  – соответствующие частоты всех интервалов статистического ряда, то выборочное среднее определяется формулой:

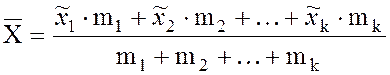, или       

.

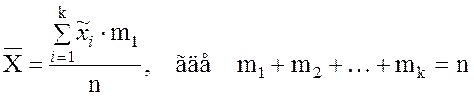Пример 2.10 Найдем выборочное среднее возраста пациентов поликлиники по данным статистического ряда из примера 1.3.

Таблица 2.9 – Данные исследования возраста пациентов             поликлиники