Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 9

Вывод. Найденные характеристики выборки определяют расположение и разброс данных. Значения эксцесса  и асимметрии  позволяют выдвинуть предположение о «более» острой вершине и правосторонней асимметрии плотности вероятностей случайной величины  относительно нормального распределения с теми же параметрами.

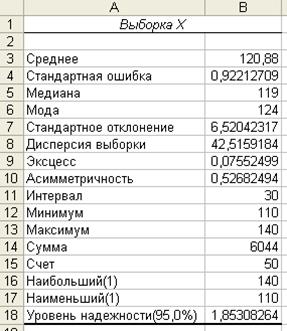
Рис. 1. Результат анализа

Описательная статистика

2. Нахождение точечной оценки параметра  показательного распределения. Метод моментов.Поскольку плотность распределения вероятностей нормального распределения:

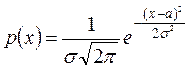
зависит от двух неизвестных параметров  и , то находятся начальные теоретические моменты первого и второго порядков

,

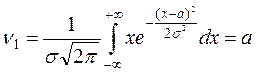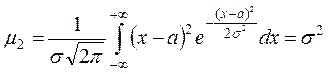
и соответствующие выборочные

, .

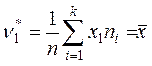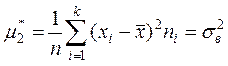Согласно методу моментов приравниваем

, .

Значение оценки параметра  получено в Описательной статистике в строке Среднее. Оценка параметра  получается по формуле

=(СЧЕТ–1)/СЧЕТ*ДИСПЕРСИЯ ВЫБОРКИ.

Метод максимально правдоподобия. Для нормального распределения вероятностей

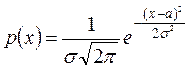
составляется функция правдоподобия

,

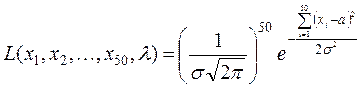логарифмическая функция правдоподобия которой имеет вид:

.

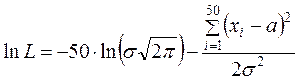Данная функция исследуется на экстремум:

– находятся частные производные первого порядка:

, ,

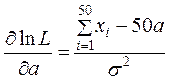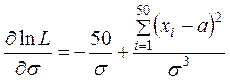– находится точка экстремума, приравнивая частные производные к нулю:

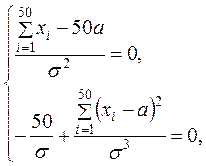
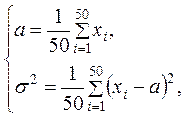
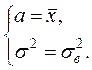
Следовательно, в качестве точечных оценок неизвестных параметров  и  нормального распределения берутся  и .

3. Интервальные оценки. Пусть  – выборка из генеральной совокупности значений нормально распределенной случайной величины ~, где = и .

Доверительный интервал для  при известной . Результаты нахождения доверительного интервала представлены в виде таблицы в среде MS Excel (рис. 2).

Рис. 2. Границы доверительного интервала

для  при известной

Содержимое ячеек заполняется следующим образом:

·  в ячейки B1-B3 копируются данные из Описательной статистики;

·  ячейка В4 содержит формулу

=ДОВЕРИТ(0,05;B3;B1);

·  ячейка В5 содержит формулу =B2–B4;

·  ячейка В6 содержит формулу =B2+B4.

Вывод. Доверительный интервал (119,07;122,69) накрывает с вероятностью 0,95 математическое ожидание  случайной величины  при известной дисперсии . Значит, средний расход используемого сырья по данной технологии (математическое ожидание) находится в указанном интервале в 95% случаев наблюдений и только в 5% параметр может выйти из этого интервала.

Доверительный интервал для  при неизвестной . Результаты нахождения доверительного интервала представлены в виде таблицы в среде MS Excel (рис. 3).

Рис. 3. Границы доверительного интервала

для  при неизвестной

Содержимое ячеек заполняется следующим образом:

·  в ячейки B1-B3 копируются данные из Описательной статистики;

·  ячейка В4 содержит формулу

=СТЬЮДРАСПОБР(0,05;B1-1);

·  ячейка В5 содержит формулу =B4*B3/КОРЕНЬ(B1);

·  ячейка В6 содержит формулу =B2–B5;

·  ячейка В7 содержит формулу =B2+B5.

Замечание. В ячейку B6 можно сразу вписать формулу

=B2- СТЬЮДРАСПОБР(0,05;B1-1)*B3/КОРЕНЬ(B1).

Аналогично, с ячейкой B7.

Вывод. Доверительный интервал (119,027;122,733) накрывает с вероятностью 0,95 математическое ожидание = при неизвестной дисперсии .

Доверительный интервал для  при известном . Результаты нахождения доверительного интервала представлены в виде таблицы в среде MS Excel (рис. 4).

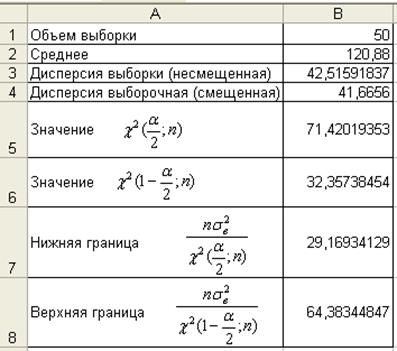
Рис. 4. Границы доверительного интервала

для  при известном

Содержимое ячеек заполняется следующим образом:

·  в ячейки B1-B3 копируются данные из Описательной статистики;

·  ячейка В4 содержит формулу =(B1-1)*B3/B1 или значение выборочной дисперсии , предварительно вычисленное с помощью функции

ДИСПР(число1;число2;…);

·  ячейка В5 содержит формулу

=ХИ2ОБР(0,05/2;B1);

·  ячейка В6 содержит формулу

=ХИ2ОБР(1-(0,05/2);B1);

·  ячейка В7 содержит формулу =B1*B4/B5;

·  ячейка В8 содержит формулу =B1*B4/B6.

Замечание. В ячейки B7 и B8 можно сразу вписать соответственно формулы:

=B1*(B1-1)*B3/B1*ХИ2ОБР(0,05/2;B1),

=B1*(B1-1)*B3/B1*ХИ2ОБР(0,05/2;B1).