Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 10

Вывод. Доверительный интервал (29,169;64,383) накрывает с вероятностью 0,95 дисперсию  при известном математическом ожидании .

Доверительный интервал для  при неизвестном . Результаты нахождения доверительного интервала представлены в виде таблицы в среде MS Excel (рис. 5).

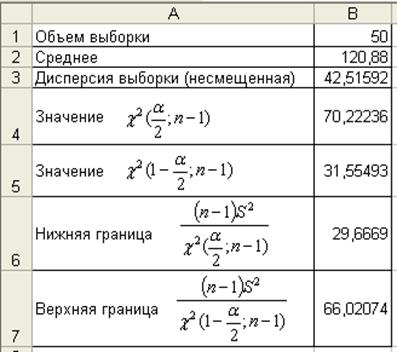
Рис. 5. Границы доверительного интервала

для  при неизвестном

Содержимое ячеек заполняется следующим образом:

·  в ячейки B1-B3 копируются данные из Описательной статистики;

·  ячейка В4 содержит формулу

=ХИ2ОБР(0,05/2;B1-1);

·  ячейка В5 содержит формулу

=ХИ2ОБР(1-(0,05/2);B1-1);

·  ячейка В6 содержит формулу =(B1-1)*B4/B5;

·  ячейка В7 содержит формулу =(B1-1)*B4/B6.

Замечание. В ячейки B6 и B7 можно сразу вписать формулы соответственно:

=B1*(B1-1)*B3/B1*ХИ2ОБР(0,05/2;B1),

=B1*(B1-1)*B3/B1*ХИ2ОБР(0,05/2;B1).

Вывод. Доверительный интервал (29,67;66,02) накрывает с вероятностью 0,95 дисперсию  при неизвестном математическом ожидании .

Тема 3

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

О ПАРАМЕТРАХ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ

ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ

1  Основные понятия

2  -значение

3  Проверка статистических гипотез

4  Лабораторная работа

1. Основные понятия. Пусть  – наблюдаемая дискретная или непрерывная случайная величина. Статистической гипотезой  называется утверждение, в котором высказывается предположение относительно параметров или вида распределения случайной величины . Гипотеза  называется простой, если она содержит только одно предположение, а гипотеза, которая состоит из конечного или бесконечного числа простых гипотез, называется сложной.Гипотезы о значениях параметров известного распределения случайной величины  называются параметрическими. Непараметрическими называются гипотезы, сформулированные относительно вида закона распределения случайной величины . Основная выдвинутая гипотеза называется нулевой . Гипотеза, противоречащая нулевой гипотезе , называется альтернативной (конкурирующей) гипотезой . Выбор альтернативной гипотезы определяется конкретной формулировкой задачи [2].

Правило, по которому принимается решение принять или отклонить гипотезу , называется критерием K. Случайная величина , с помощью которой принимают решение о принятии или отклонении нулевой гипотезы, называется статистикой  критерия K. Проверка статистической гипотезы основывается на принципе отношения правдоподобия: маловероятные события считаются невозможными, а события, имеющие большую вероятность, считаются достоверными. Зафиксируем некоторую малую вероятность  – уровень значимости. Пусть  – множество значений статистики ,  – такое подмножество, для которого

=.

Наблюдаемым значением  называется значение статистики , вычисленное по выборке  из генеральной совокупности случайной величины . Правило проверки статистических гипотез состоит в следующем:

если , то гипотеза  отклоняется с вероятностью

=,

если , то гипотеза  принимается с вероятностью

=1–.

Критерий, основанный на использовании заранее заданного уровня значимости , называется критерием значимости. Вероятность  называется доверительной вероятностью.

Критической областью  называется совокупность значений статистики , при которых нулевую гипотезу отвергают. Областью принятия гипотезы называется совокупность значений  статистики , при которых нулевая гипотеза принимается. Критическими точками  называются точки, отделяющие критическую область  от области принятия гипотезы . Уровень значимости  определяет «размер» критической области . Положение критической области на множестве статистики  зависит от вида нулевой и альтернативной гипотез. Возможны три вида расположения критической области [15]:

– правосторонняя критическая область ;

– левосторонняя критическая область ;

– двусторонняя критическая область

.

Точки ,  определяются в зависимости от вида закона распределения статистики  при выбранном уровне значимости .

Выбор между гипотезами  и  может сопровождаться ошибками двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная нулевая гипотеза . Вероятность ошибки первого рода равна уровню значимости: