Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 18

·  Альфа – вводится уровень значимости 0,05;

·  Выходной диапазон– вводится ссылка на новый рабочий лист «t-тест-одинак-дисп».

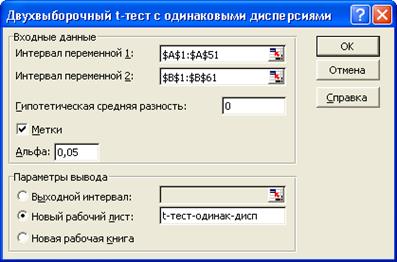
Рис. 5. Заполнение диалогового окна

Двухвыборочный -тест с одинаковыми дисперсиями

На рисунке 6 представлены рассчитанные в данном режиме показатели.

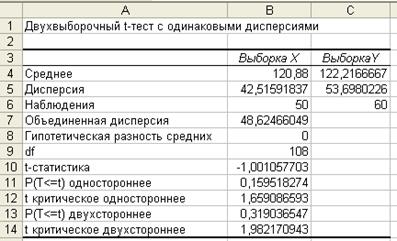
Рис. 6. Результаты проверки гипотезы  ,

где  и  неизвестны и

Вывод. Наблюдаемое значение  попадает в область допустимых значений, т.е. 1,001==1,982, поэтому нет оснований отвергнуть нулевую гипотезу : на уровне значимости 0,05 при альтернативной гипотезе , . Для -значения имеет место неравенство 0,319>0,05, что также говорит о хорошем согласии с .

При альтернативной гипотезе  имеем:

=1,001<1,6591=, =0,1595>0,05,

значит, гипотеза : отвергается при уровне значимости =0,05. При альтернативной гипотезе  имеем:

= –1,001> –1,6591=, =0,1595>0,05,

значит, гипотеза : принимается при уровне значимости =0,05.

4. Проверка гипотезы о равенстве математических ожиданий при неизвестных и неравных дисперсиях.По выборкам  и  значений нормально распределенных случайных величин ~ и ~ выдвигается гипотеза о равенстве математических ожиданий:

:,

в предположении, что  и  неизвестны и неравны, при одной из альтернативных гипотез :

1) , ,

2) ,

3) .

Для проверки данной гипотезы используется режим анализа Двухвыборочный -тест с различными дисперсиями. Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис. 7):

·  Интервал переменной 1 – вводятся ссылки на ячейки А1:А51, в которых находятся значения выборки ;

·  Интервал переменной 2 – вводятся ссылки на ячейки С1:С61, в которых находятся значения выборки ;

·  Гипотетическая средняя разность – вводится число 0;

·  Метки – устанавливается флажок;

·  Альфа – вводится уровень значимости 0,05;

·  Выходной диапазон– вводится ссылка на новый рабочий лист «t-тест-различ-дисп».

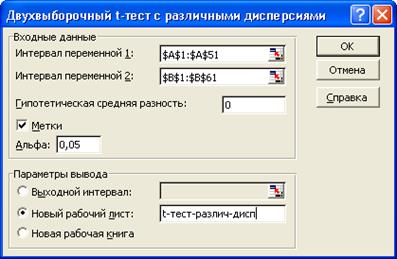
Рис. 7. Заполнение диалогового окна

Двухвыборочный -тест с различными дисперсиями

На рисунке 8 представлены рассчитанные в данном режиме показатели.

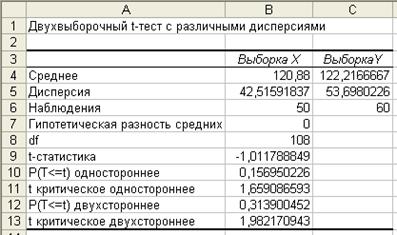
Рис. 8. Результаты проверки гипотезы  ,

где  и  неизвестны и

Вывод. Наблюдаемое значение  попадает в область допустимых значений, т.е. 1,0118==1,9832. Поэтому нет оснований отвергнуть нулевую гипотезу : на уровне значимости 0,05 при альтернативной гипотезе , . Для -значения имеет место неравенство 0,3139>0,05, что также говорит о хорошем согласии с .

При альтернативной гипотезе  имеем:

=1,0118<1,6591=, =0,1569>0,05,

значит, гипотеза : также принимается при уровне значимости =0,05. При альтернативной гипотезе  имеем

= –1,0118>–1,6591=, = 0,1569>0,05.

Значит, гипотеза : также принимается при уровне значимости =0,05.

5. Проверка гипотезы о равенстве дисперсий нормальных выборок при неизвестных математических ожиданиях.По выборкам  и  значений нормально распределенных случайных величин ~ и ~ с неизвестными математическими ожиданиями , , выдвигается гипотеза

:,

при альтернативной гипотезе , которая может быть одной из следующих:

1)  (если ), или  (если ),

2) .

Для проверки данной гипотезы используется режим работы Двухвыборочный -тест для дисперсии. Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис.9):

·  Интервал переменной 1 – вводятся ссылки на ячейки А1:А51, в которых находятся название и значения выборки ;

·  Интервал переменной 2 – вводятся ссылки на ячейки С1:С61, в которых находятся название и значения выборки ;

·  Гипотетическая средняя разность – вводится число 0;

·  Метки – устанавливается флажок;

·  Альфа – вводится уровень значимости 0,05;

·  Выходной диапазон– вводится ссылка на новый рабочий лист «F-тест».

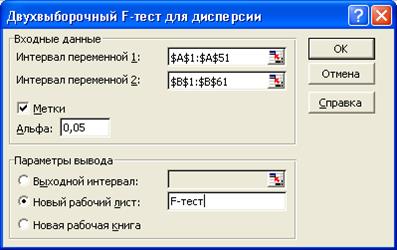
Рис. 9. Заполнение диалогового окна

Двухвыборочный -тест для дисперсии

В выбранном выходном диапазоне A1:C10 появится результат анализа, представленный на рисунке 10.

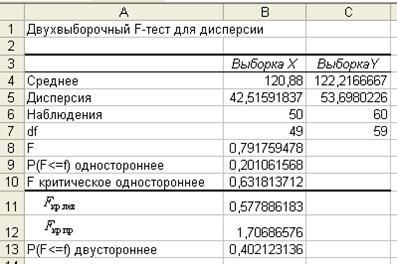
Рис. 10. Результаты проверки гипотезы 

:, где ,  неизвестны