Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 4

В режиме Гистограмма выполняются статистические анализы Парето, Интегральный процент, Вывод графика.

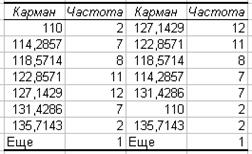
Если устанавливается флажок Парето (отсортированная гистограмма), то в выходном диапазоне появится гистограмма и отсортированная гистограмма (рис. 5).

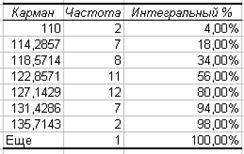
Если устанавливается флажок Интегральный процент, то в выходном диапазоне появляется накопляемый процентный вклад каждого интервала значений вариант, представляющий собой процентное выражение эмпирической функции распределения (рис. 6).

                    

Рис. 5. Результат анализа                 Парето

Рис. 6. Результат анализа             Интегральный процент

Если устанавливается флажок Вывод графикa, то выводится интервальный ряд и гистограмма (рис. 7).

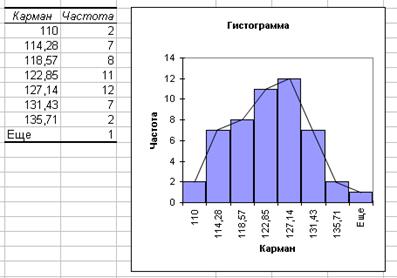
Рис. 7. Результат анализа Вывод графика

Замечания. 1. В ячейках Кармана можно изменить формат чисел, оставив два знака после запятой (выделяются ячейки, затем в командной строке выбирается Формат–Ячейки…–Число–Числовой–Число десятичных знаков ).

2. Для того чтобы гистограмма приняла стандартный вид (столбики гистограммы изображались в виде смежных прямоугольных областей), необходимо выбрать Область диаграммы–Ряд «Частота»–Формат рядов данных–Параметры–Ширина зазора , командами Область построения диаграммы–Вид–Заливка–Прозрачная изменяется фон области построения диаграммы.

3. При необходимости гистограмма интервального ряда может быть преобразована в полигон. Для этого нужно соединить середины верхних сторон прямоугольников прямыми линиями (ломаная линия на рисунке 7 получена с помощью команды Рисование–Линия  на панели инструментов Рисование).

При установленных флажках Парето, Интегральный процент, Вывод графика результаты анализов получается таблица, гистограмма и кумулятивная кривая (рис. 8).

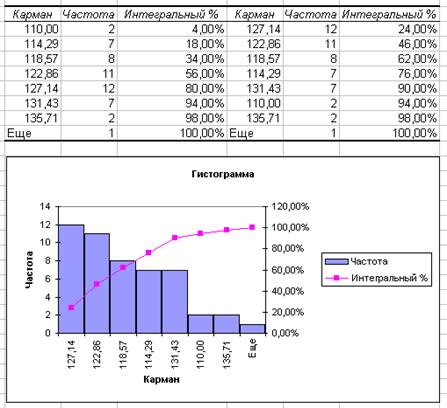
Рис. 8. Результат анализов Парето,

 Интегральный процент, Вывод графика

Вывод. По виду гистограммы, изображенной на рисунке 7, можно предположить, что случайная величина  расхода сырья при производстве продукции по данной технологии имеет нормальное распределение.

Тема 2

ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

1  Числовые характеристики выборки

2  Точечные оценки параметров распределения

3  Интервальные оценки параметров распределения

4  Лабораторная работа

1. Числовые характеристики выборки. Пусть случайный эксперимент описывается случайной величиной , распределение которой зависит от одного или несколько параметров. К ним, в частности, относятся среднее, мода, медиана, среднее квадратичное отклонение, дисперсия, коэффициенты эксцесса и асимметрии, размах вариации, называемые параметрами генеральной совокупности. При исследовании случайной величины  из генеральной совокупности ее возможных значений извлекается выборка  объема . По данной выборке можно приближенно вычислить значения каждого из изучаемых параметров, которые в статистике называются числовыми оценками параметров или просто оценками. Данные характеристики условно разбиваются на три группы:

– показатели положения вариант на числовой оси,

– показатели разброса вариант относительно своего центра, определяющие кучность данных около центра,

– показатели асимметрии распределения вариант около своего центра,

– показатели, описывающие закон распределения (тема 3).

Пусть выборка  задана вариационным рядом (таблица 1).

Таблица 1 Вариационный ряд

Варианты
Относительные частоты

Выборочным средним значений выборки называется число, определяемое по формуле

,

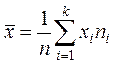где  – варианта с частотой ,  – число наблюдений, 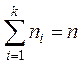. Если частоты  равны единице, то . При достаточно больших  используют формулу:

,

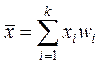где  – число значений вариационного ряда,  – относительная частота варианты . Если известен интервальный вариационный ряд, то для вычисления выборочного среднего используется формула:

,

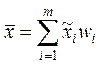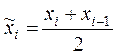где  – число интервалов,  – середина i-го интервала,  – относительная частота.