Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 2

Пусть . Выборочной квантилью порядка  называется абсцисса  точки, лежащей на кумулятивной кривой и имеющей ординату  (рисунок 1).

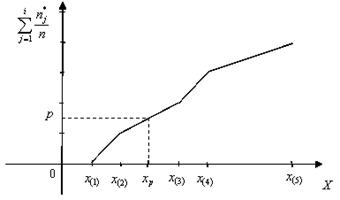
Рис. 1. Выборочная квантиль порядка p.

Порядок квантили  определяет долю общего числа вариант в выборке, результаты которых не превосходят .

Процентным выражением кумулятивной кривой является интегральный процент, показывающий накопляемый процентный вклад каждого интервала значений величины .

По виду полигона или гистограммы обычно выдвигают предположение о виде закона распределения исследуемой случайной величины, что позволяет придать определенную направленность исследованиям.

3. Эмпирическая функция распределения и кумулятивная кривая. Статистической (эмпирической) функцией распределения выборки называется функция  действительного аргумента , определяющая относительную частоту события :

,

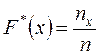где  – число вариант, меньших .

Основными свойствами статистической функции распределения выборки являются:

1) ;

2) функция  является неубывающей;

3)  при  и  при , где  и  – соответственно наименьшее и наибольшее значения выборки.

Если известен вариационный ряд выборки, то статистическая функция распределения определяется как

.

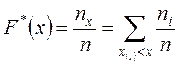Для построения статистической функции распределения  в случае известного интервального ряда осуществляется переход к вариационному ряду с равноотстоящими или неравноотстоящими вариантами.

Работа в Excel. Для построения вариационного ряда и полигона частот используются соответственно инструменты Сортировка по возрастанию  и Мастер диаграмм.

.

Таблица 4. Интервальный ряд

Карман (левые концы интервалов)	Частота
	– число вариант, от  до
	– число вариант, от  до
	– число вариант, от  до
Еще	– число вариант, от  до

Для нахождения интегрального ряда, кумулятивной кривой, гистограммы используется Гистограмма из пакета Анализ данных меню Сервис (приложение 2). Результат анализа появляется в виде таблицы. Формулы и соответствующие функции Excel, по которым выполняются расчеты в данном режиме, приводится в таблице 4.

Таблица 5. Формулы для расчета результатов статистических анализов Парето, Интегральный процент, Вывод графика

1	2	3	4	5	6
Карман1	Частота2	Интегральный % 3	Карман4	Частота5	Интегральный % 6
	– число вариант, от  до			– наиб. частота
	– число вариант, от  до
	– число вариант, от  до
Еще	– число вариант, от  до			– наименьшая частота

1 – левый конец каждого интервала,

2 – число вариант, содержащихся в соответствующем интервале,

3 – процентное выражение накопленных частот для интервалов,

4 – правые концы интервалов, расположенные в порядке убывания частот;

5 – частоты, расположенные в порядке убывания,

6 – процентное выражение накопленных частот, расположенных в порядке убывания.

В таблице 5 приводятся формулы, по которым проводятся расчеты в Excel для выполнения статистических анализов:

– Парето (столбцы 1, 2, 4, 5);

– Интегральный процент (столбцы 1, 2, 3);

– Парето и Вывод графика (столбцы 1, 2, 4, 5), при этом выводится гистограмма частот, расположенных в порядке убывания;

– Парето, Интегральный процент и Вывод графика появляется таблица 5, гистограмма частот, расположенных в порядке убывания, и график кумулятивной кривой, соответствующей интегральному проценту.

Вопросы для самоконтроля

1. Что называется вариационным рядом?

2. Как строится интервальный ряд?

3. Какой ряд называется интервальным вариационным рядом с равноотстоящими вариантами?

2. Как строится гистограмма?

3. Что называется кумулятивной кривой?