Для проверки гипотезы ![]() :
:![]() =0 при альтернативной гипотезе
=0 при альтернативной гипотезе ![]() :
:![]()
![]() 0 используется наблюдаемое значение
0 используется наблюдаемое значение ![]() -статистики
-статистики ![]() =273,74,
находящееся в ячейке Е12. Критическое значение
=273,74,
находящееся в ячейке Е12. Критическое значение ![]() статистики
вычисляется в ячейке D33 по формуле
статистики
вычисляется в ячейке D33 по формуле
=FРАСПОБР(0,05;В12;В13),
после
выполнения анализа Регрессия и равно ![]() =9,55.
=9,55.
Поскольку 273,74=![]() >
>![]() =9,55, то нулевая гипотеза отклоняется,
т.е. коэффициент детерминации является значимым. Для
=9,55, то нулевая гипотеза отклоняется,
т.е. коэффициент детерминации является значимым. Для ![]() -значения
имеет место неравенство
-значения
имеет место неравенство ![]()
![]() =0,0004<0,05,
что также подтверждает значимость коэффициента детерминации (
=0,0004<0,05,
что также подтверждает значимость коэффициента детерминации (![]() -значение находится в ячейке F12 –
Значимость F).
-значение находится в ячейке F12 –
Значимость F).
Вычисление показателя средней ошибки аппроксимации ![]() осуществляется также после выполнения
анализа Регрессия. Для этого осуществляются следующие операции:
осуществляется также после выполнения
анализа Регрессия. Для этого осуществляются следующие операции:
– в ячейки А34:А39 вводятся значения результативного признака
![]() (прибыль);
(прибыль);
– в ячейку D35 вводится формула массива
{=(СУММ(ABS(C26:C31)/(A34:A39))/6)*100},
где C26:C31 – ячейки, содержащие остатки, т.е. разности между эмпирическими и теоретическими значениями результативного признака.
В результате получается значение ![]() =2,699%, подтверждающее достаточно высокую
адекватность построенного уравнения регрессии.
=2,699%, подтверждающее достаточно высокую
адекватность построенного уравнения регрессии.
Проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов. Для проверки гипотез
![]() :
:![]() =0,
=0, ![]() =0,
=0, ![]() =0,
=0,
при альтернативных гипотезах
![]() :
:![]() ,
, ![]()
в анализе Регрессия рассчитываются
в ячейках D17:19 наблюдаемые значения ![]() -статистики:
-статистики:
для
![]() :
: ![]() =-9,8721,
=-9,8721,
для
![]() :
: ![]() =3,5303,
=3,5303,
для
![]() :
: ![]() =5,7485.
=5,7485.
Поскольку в таблицах не
приводится значение ![]() , то оно вычисляется после выполнения анализа Регрессия в ячейке D37 по формуле:
, то оно вычисляется после выполнения анализа Регрессия в ячейке D37 по формуле:
=СТЬЮДРАСПОБР(0,05;6-2-1)
и равно ![]() =3,1824.
Здесь 0,05 – уровень значимости, 6 – число наблюдений, 2 – число факторов в
уравнении регрессии, 1 – число свободных членов в уравнении регрессии.
=3,1824.
Здесь 0,05 – уровень значимости, 6 – число наблюдений, 2 – число факторов в
уравнении регрессии, 1 – число свободных членов в уравнении регрессии.
Так как
![]()
![]()
![]() ,
,
то коэффициент ![]() не является значимым.
не является значимым.
Коэффициенты
![]() и
и ![]() попадают
в критическую область
попадают
в критическую область
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
поэтому они являются значимыми.
Найденные коэффициенты ![]() ,
, ![]() ,
, ![]() (ячейки
В17:В19) сравниваются попарно с их стандартными ошибками
(ячейки
В17:В19) сравниваются попарно с их стандартными ошибками ![]() ,
, ![]() ,
, ![]() (ячейки С17:19). Для коэффициента
(ячейки С17:19). Для коэффициента ![]() имеем неравенство
имеем неравенство ![]() <
<![]() . Стандартные ошибки коэффициентов
. Стандартные ошибки коэффициентов ![]() ,
, ![]() меньше
своих стандартных ошибок,
меньше
своих стандартных ошибок, ![]() >
>![]() ,
, ![]() >
>![]() .
. ![]() -значения
коэффициентов
-значения
коэффициентов ![]() ,
, ![]() ,
, ![]() удовлетворят неравенствам:
удовлетворят неравенствам:
![]() :
: ![]() =0,8153>0,05=
=0,8153>0,05=![]()
![]() :
: ![]() =0,0386
=0,0386![]() 0,05=
0,05=![]() ,
,
![]() :
: ![]() =0,0104
=0,0104![]() 0,05=
0,05=![]() ,
,
что
также говорит о незначимости коэффициента ![]() и о
значимости коэффициентов
и о
значимости коэффициентов ![]() ,
, ![]() .
.
Из предварительного
анализа уравнения регрессии следует, что его необходимо пересчитать без
свободного члена ![]() , который не является
статистически значимым.
, который не является
статистически значимым.
Для пересчета уравнения регрессии в диалоговом окне Регрессия задаются те же параметры, при этом устанавливается флажок активизации параметра Константа-ноль (рис.9):
После пересчета на новом рабочем листе Регрессия пересчет генерируются таблицы (рис.10), аналогичные таблицам, изображенным на рисунке 8.
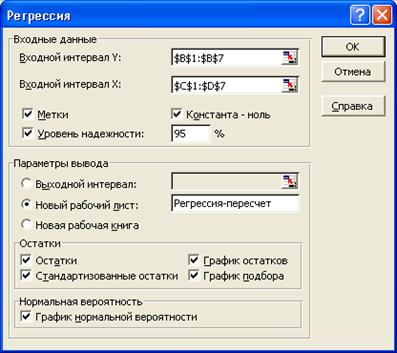
Рис.9. Заполнение диалогового окна Регрессия
при условии ![]() =0
=0
Таким образом, получается новое уравнение регрессии:
![]() .
.
Для нового
выборочного коэффициента детерминации ![]() =0,9944
аналогично предыдущим рассуждениям имеем:
=0,9944
аналогично предыдущим рассуждениям имеем:
357,211=![]() >
>![]() =9,55,
=9,55,
![]()
![]() =0,00027<0,05.
=0,00027<0,05.
Значит, ![]() является
значимым.
является
значимым.
Для коэффициентов ![]() ,
, ![]() при
факторных признаках наблюдаемые значения
при
факторных признаках наблюдаемые значения ![]() -статистики
принадлежат критический области:
-статистики
принадлежат критический области:
5,94654=![]()
![]()
![]() ,
,
7,6520=![]()
![]()
![]() ,
,
значит, они являются значимыми.
Значения коэффициентов ![]() ,
, ![]() больше своих стандартных ошибок:
больше своих стандартных ошибок:
![]() =0,6564>0,11039=
=0,6564>0,11039=![]() ,
,
![]() =0,2066>0,0270=
=0,2066>0,0270=![]() ,
,
и ![]() -значения коэффициентов
-значения коэффициентов ![]() ,
, ![]() удовлетворят
неравенствам:
удовлетворят
неравенствам:
![]() :
: ![]() =0,0040
=0,0040![]() 0,05=
0,05=![]() ,
,
![]() :
:![]() =0,0015
=0,0015![]() 0,05=
0,05=![]() ,
,
что
говорит о значимости коэффициентов ![]() ,
, ![]() .
.
Итак, полученное уравнение регрессии адекватно экспериментальным данным.
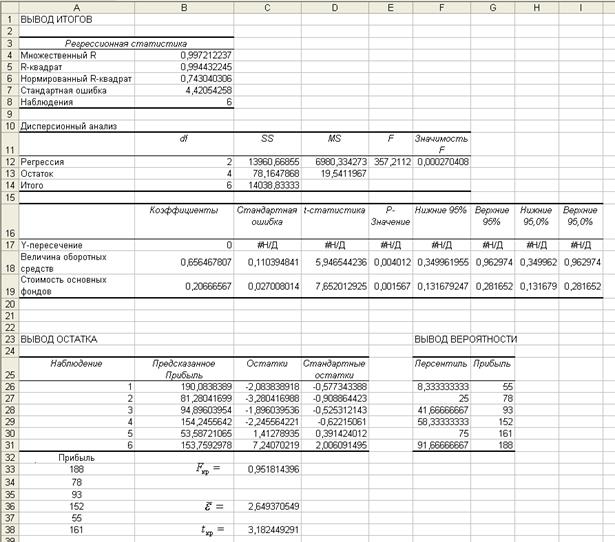
Рис. 10. Результат анализа Регрессия
(пересчет уравнения регрессии)
Итак, полученное уравнение регрессии адекватно экспериментальным данным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.