Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 16

Выборка :

109	137	111	133	111	126	111	114	114	114
119	122	119	122	122	122	119	122	122	122
114	119	114	114	119	119	114	119	119	119
122	123	122	123	123	123	122	123	123	123
123	133	123	111	126	126	126	126	126	126
133	114	133	133	111	135	133	135	135	137

Требуется при заданном уровне значимости  проверить следующие гипотезы:

1) о нормальном законе распределения генеральной совокупности случайной величины , используя критерии Пирсона и Колмогорова;

2) о равенстве математических ожиданий двух нормальных генеральных совокупностей, дисперсии которых известны и равны;

3) о равенстве математических ожиданий двух нормальных генеральных совокупностей, дисперсии которых неизвестны и равны;

4) о равенстве математических ожиданий двух нормальных генеральных совокупностей, дисперсии которых неизвестны и различны;

5) о равенстве дисперсий двух нормальных генеральных совокупностей, математические ожидания которых неизвестны.

Порядок выполнения работы

1. Проверка гипотезы о законе распределения. Критерий Пирсона.По выборке  значений случайной величины  при заданном уровне значимости  выдвигается гипотеза

,

где  – известная функция нормального распределения:

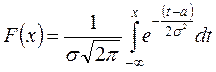
с параметрами  и . При достаточно большом объеме выборки  в качестве оценок  и  используются ,  соответственно.

Расчеты по нахождению  представлены в виде таблицы в среде MS Excel (рис. 1), используя результаты анализов Описательная статистка (практическая работа темы 4) и Гистограмма (практическая работа темы 3).

Содержимое ячеек заполняется следующим образом:

·  в ячейки А3:А10 копируется столбец Карман из Гистограммы (практическая работа темы 3), заменяется Еще на число в 2-3 раза большее Максимума из Описательной статистики, поскольку правый конец последнего интервала – неопределенность ;

·  в ячейки В3:В10 копируется Частоты из Гистограммы,

·  в ячейки В11, В12, В13 копируются значения Среднее, Стандартное отклонение и Счет из Описательной статистки соответственно,

·  ячейки С3:С10 содержат формулу

{=НОРМРАСП(А3:А10;В11;В12;ИСТИНА)},

а в ячейку С2 вводится значение 0 (так как );

·  ячейки D3:D10 содержат формулу

{=C3:C10-C2:C9};

·  ячейки E3:E10 содержат формулу

{=B13*D3:D10};

·  ячейки F3:F10 содержат формулу

{=(B3:B10-E3:E10)^2/E3:E10};

·  ячейка В14 содержит формулу

=СУММ(F3:F10);

·  ячейка В15 содержит формулу

=ХИ2ОБР(0,05; 8-2-1).

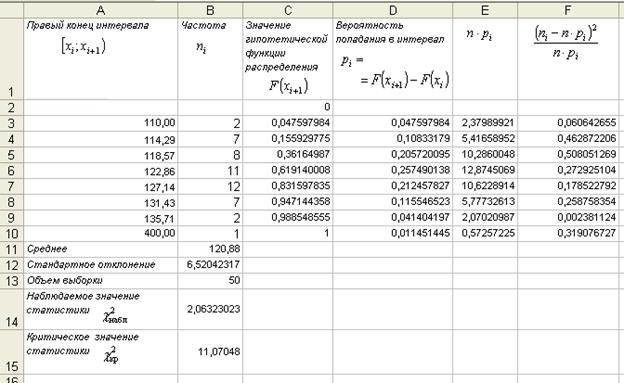
Рис. 1. Проверка гипотезы о законе распределения

с помощью критерия Пирсона

Вывод. Так как =2,0632311,07048, то нет оснований для отклонения нулевой гипотезы о нормальном распределении случайной величины  с параметрами 120,88, =6,52. Значит, предположение о нормальном законе расхода сырья при производстве продукции верно в 95% случаев наблюдений.

Критерий Колмогорова. По выборке  значений случайной величины  при заданном уровне значимости  выдвигается гипотеза

,

где  – известная нормальная функция распределения

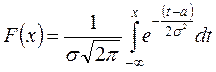
с параметрами  и . При достаточно большом объеме выборки  в качестве оценок  и  используются ,  соответственно.

Результаты нахождения  представлены в виде таблицы в среде MS Excel (рис.2), используя результаты анализов Описательная статистка (практическая работа темы 4) и Гистограмма (практическая работа темы 3).

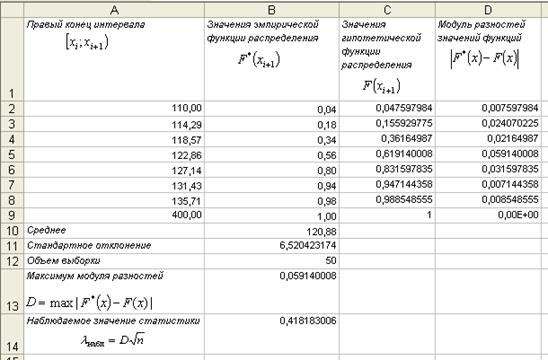
Рис. 2. Проверка гипотезы о законе распределения

с помощью критерия Колмогорова

Содержимое ячеек заполняется следующим образом:

·  в ячейки A2:A9 копируется столбец Карман из Гистограммы, заменяется Еще на число в 2-3 раза большее Максимума из Описательной статистики, поскольку правый конец последнего интервала есть неопределенность ;