Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 29

Проверка данных гипотез осуществляется с помощью -статистики:

, ,

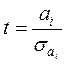имеющей распределение Стьюдента с к  числом степеней свободы. Здесь , , – стандартные значения ошибок для коэффициентов регрессии  соответственно.

По выборочным данным вычисляется наблюдаемое значение -статистики , по таблицам критических точек распределения Стьюдента находятся критические значения =. Если  попадает в критическую область, т.е. , то нулевая гипотеза :, , отвергается.

Доверительные интервалы для каждого коэффициента , , регрессии имеют вид:

, .

Если незначимым окажется коэффициент , проводится пересчет уравнения регрессии в предположении, что =0. Если же незначимым окажется коэффициент при факторе, то следует пересмотреть набор факторов в уравнении регрессии.

Коэффициенты , , …,  при факторах , , …, показывают степень влияния каждого фактора на результативный признак .

При практической интерпретации уравнения регрессии также широко используются частные коэффициенты эластичности, показывающие, на сколько процентов в среднем изменится значение результативного признака  при изменении значения соответствующего фактора  на 1%, и определяемые по формуле

,

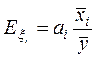где  – среднее значение соответствующего фактора ;  – среднее значение результативного признака ;  – коэффициент регрессии при соответствующем факторе.

Работа в Excel. Для нахождения коэффициентов множественной регрессии, множественного коэффициента детерминации, ковариационной матрицы используется режим Регрессия из Анализа данных меню Сервис (Приложение 2). Результат анализа ВЫВОД ИТОГОВ представлен в виде пяти таблиц: Регрессионная статистика, Дисперсионный анализ, таблицы, содержащей коэффициенты регрессии и их статистические оценки, Вывод остатка и Вывод вероятности. Формулы и функции Excel, по которым рассчитываются соответствующие числовые значения, приводятся в таблицах 4, 5, 6, 7, 8.

Таблица 4. Результат анализа Регрессия:Регрессионная статистика

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный (коэффициент корреляции)	, КОРРЕЛ
- квадрат (коэффициент детерминации)
Нормированный  - квадрат
Стандартная ошибка (остаточное стандартное отклонение)	ЛИНЕЙН(с аргументом статистика=1)
Наблюдения (число наблюдений)	СЧЕТ

Таблица 5. Продолжение анализа Регрессия: Дисперсионный анализ

Дисперсионный анализ
	Регрессия	Остаток	Итого
Число степеней свободы df	=	=	=+
	=
Значимость	Значение уровня значимости, при соответствующем   FРАСП(;;)

Замечание. В Excel на экран выводится таблица, строки которой записаны в столбцах таблицы 4.

Таблица 6. Результат анализа Регрессия: коэффициенты регрессии и их статистические оценки

	-пересечение	Переменная	…	Переменная
Коэффициенты			…
Стандартная ошибка			…
-статистика (наблюдаемые значения статистики)	=	=	…	= =
-значение (значения уровня значимости, соответствующие вычисленным значениям статистики)	СТЬЮДРАСП (;n-m-1)	СТЬЮДРАСП (;n-m-1)	…	СТЬЮДРАСП (;n-m-1)
Нижние 95% (нижние границы доверительных интервалов)	-	-	…	-
	=СТЬЮДРАСПОБР(;n-m-1)
Верхние 95% (верхние границы доверительных интервалов)	+	+	…	+
	=СТЬЮДРАСПОБР(;n-m-1)

Замечание. В Excel на экран выводится таблица, строки которой записаны в столбцах таблицы 6.