Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 5

Выборочной медианой называется значение признака, находящегося в середине вариационного ряда. Если число вариант нечетно, т. е. , то медианой является ()-я варианта (); если же число вариант четно, то медиана равна среднему арифметическому двух значений в середине ряда:

.

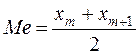Если известен интервальный вариационный ряд, то медианой является выборочная квантиль  (см. тему 2). Оценка медианы по интервальному ряду с одинаковой длиной интервалов  может быть вычислена по формуле

,

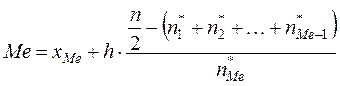где  – нижняя граница интервала, к которому принадлежит медиана,  – число элементов выборки в этом интервале,  – число элементов выборки в интервалах, лежащих слева от интервала, содержащего медиану.

Выборочной модой (Мо)называется варианта выборки, имеющая наибольшую частоту. Если несколько соседних значений имеют наибольшую частоту, то модой является их среднее арифметическое:

,

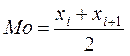где для вариант  частоты . Если две или более несмежных вариант имеют разные наибольшие частоты, то ряд называется полимодальным. Если же все варианты встречаются одинаково часто, то ряд моды не имеет.

Для интервального ряда, когда длина интервалов одинакова и равна , мода вычисляется по формуле

,

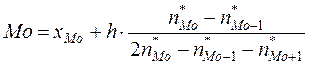где  – где нижняя граница интервала, содержащего наибольшее число элементов выборки в этом интервале,  – число элементов выборки в соседних интервалах.

Мода и медиана используются в качестве характеристики среднего положения в случае, если границы ряда нечеткие или если ряд не симметричен.

Для описания рассеивания значений случайной величины относительно выборочного среднего используются выборочная дисперсия и выборочное среднее квадратическое отклонение.

Выборочной дисперсией наблюденных значений выборки называется число, определяемое по формуле

.

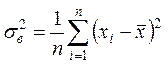После преобразований получается следующая формула:

.

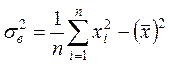Если задан вариационный ряд, то используется формула:

,

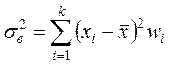где  – число вариант,  – относительная частота варианты . Если задан интервальный вариационный ряд, то

,

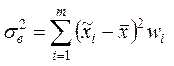где m – число интервалов,  – середина i-го интервала,  – соответствующая относительная частота.

Выборочным средним квадратическим отклонением называется число, которое находится по формуле:

.

Коэффициент вариации

,

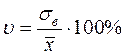характеризует относительное значение среднего квадратического отклонения и служит для сравнения колеблемости несоизмеримых показателей.

Обобщающими характеристиками выборочных распределений являются моменты вариационного ряда.

Начальным выборочным моментом -го порядка (=0,1,2,…) называется величина

,

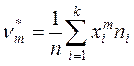где  – наблюденное значение с частотой ,  – число наблюдений, 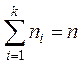. Очевидно, что , ,  и т. д.

Центральным выборочным моментом -го порядка (=0,1,2,…) называется величина

,

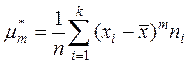где  – наблюденное значение с частотой ,  – число наблюдений, 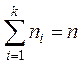,  – выборочное среднее. Очевидно, что

, , ,

, .

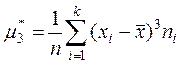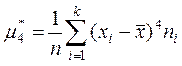Важную роль при исследовании статистических совокупностей играют асимметрия и эксцесс распределения признака, которые вычисляются соответственно по формулам:

,    .

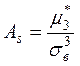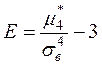Если кривая распределения симметрично относительно прямой , то распределение симметрично. Тогда  (). При асимметричном распределении вершина кривой сдвинута относительно ординаты выборочной средней. Если , то асимметрия правосторонняя (положительная), если , то – левосторонняя (отрицательная).

                                                   а)                                                                                                                                           б)

       

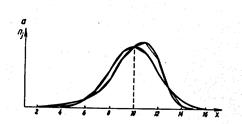
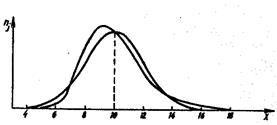
Рис. 1. Правосторонняя (а) и левосторонняя (б)

асимметричность распределения.

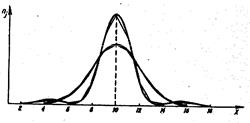
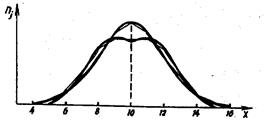
Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.

                                                   а)                                                                                                                                           б)