Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 28

Параметры уравнения регрессии определяются с помощью метода наименьших квадратов. Сущность данного метода заключается в нахождении параметров модели , , …, , при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений , , результативного признака от теоретических , , полученных по уравнению регрессии:

.

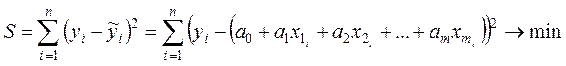Здесь  – выборка из генеральной совокупности случайной величины , .

Функция  является функцией переменных, , …, , т.е. . Исследование на экстремум данной функции проводится методами дифференциального исчисления. После несложных математических преобразований получается система  нормальных уравнений (по числу параметров)

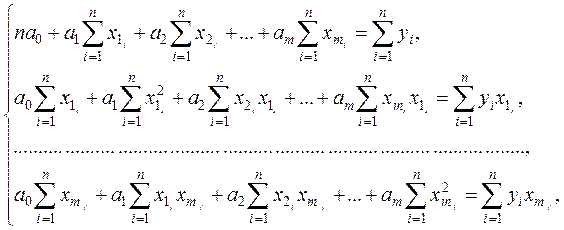
из которой находятся неизвестные , , …,  – коэффициенты уравнения регрессии. Здесь  – число наблюдений.

Этап 3. Определение степени связи результативного признака и фактора. Для определения величины степени стохастической взаимосвязи результативного признака  и факторов , , …, необходимо знать следующие дисперсии:

·  общую дисперсию результативного признака , отображающую влияние как основных, так и остаточных факторов:

,

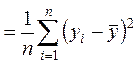где  – выборочное среднее значение результативного признака  по выборке ;

·  факторную дисперсию результативного признака , отображающую влияние только основных факторов:

;

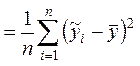·  остаточную дисперсию результативного признака , отображающую влияние только остаточных факторов:

.

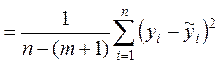При корреляционной связи результативного признака и факторов выполняется соотношение:

, при этом =+.

Этап 4. Проверка общего качества уравнения регрессии. Для анализа общего качества уравнения линейной регрессии обычно используется множественный коэффициент детерминации , называемый также квадратом коэффициента множественной корреляции. Множественный коэффициент детерминации рассчитывается по формуле

=,

и определяет долю разброса результативного признака, обусловленную изменением факторных признаков, входящих в многофакторную модель. Чем теснее линейная связь между признаками, тем ближе коэффициент детерминации к единице. Однако, при достаточно близком к единице коэффициенте детерминации не всегда наблюдается тесная взаимосвязь между случайными величинами. Поэтому необходимы дополнительные исследования.

В большинстве случаев уравнение регрессии строится на основе выборочных данных. Поэтому возникает вопрос о согласованности построенного уравнения генеральной совокупности случайного вектора . Для ответа на этот вопрос выдвигается гипотеза о незначимости множественного коэффициента детерминации:

:=0

при альтернативной гипотезе:

:0.

При проверке нулевой гипотезы используется -статистика

=,

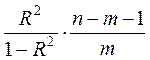имеющая распределение Фишера ,  – число наблюдений,  – число факторов в уравнении регрессии.

По выборочным данным вычисляется наблюдаемое значение статистики . По таблицам критических точек -распределения находится критическое значение статистики = =. Если  попадает в критическую область, т. е. , то нулевая гипотеза отвергается, что говорит о соответствии теоретического уравнения регрессии выборочным данным.

Для оценки адекватности уравнения регрессии также используется показатель средней ошибки аппроксимации:

.

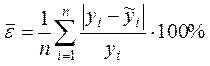Этап 5. Проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов. Возможна ситуация, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, т.е. значения данных коэффициентов будут меньше их стандартной ошибки. В этом случае такие коэффициенты должны быть исключены из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии наряду с проверкой значимости коэффициента детерминации  включает в себя также и проверку значимости каждого коэффициента регрессии.

Для этого выдвигаются нулевые гипотезы о незначимости коэффициентов , :

:, ,

при альтернативных гипотезах

:, .