Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 27

2. Оценка тесноты связи. Пусть дана выборка , , …,  из генеральной совокупности двумерной случайной величины . Оценка тесноты связи между случайными величинами  и  на основе выборочных данных проводится согласно следующему алгоритму.

1. Рассчитывается выборочный коэффициент корреляции  по одной из приведенных в пункте 1 формул.

2. Проверяется значимость (существенность) коэффициента корреляции, т.е. существенно ли  отличается от нуля или это отличие можно приписать влиянию случайности, связанной с выборкой. Для этого выдвигается нулевая гипотеза о равенстве нулю коэффициента корреляции двумерной случайной величины :

:=0

при альтернативной гипотезе:

:0.

При проверке нулевой гипотезы используется -статистика

,

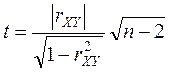имеющая распределение Стьюдента с  степенями свободы. По выборке находиться наблюдаемое значение статистики . Для заданного уровня значимости  по таблице критических точек Стьюдента определяется критическая точка . Если , то нулевая гипотеза об отсутствии корреляционной зависимости случайных величин  и  отвергается, т.е. линейный коэффициент корреляции значим, существует статистическая зависимость между случайными величинами  и .

3. Для значимого коэффициента корреляции  доверительный интервал при уровне значимости  имеет вид:

–+.

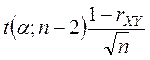
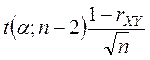4. Рассчитывается стандартная ошибка выборочного коэффициента корреляции по формуле

.

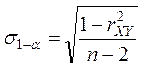Работа в Excel. Для вычисления выборочного коэффициента корреляции используется статистическая функция (Приложение 1)

КОРРЕЛ(массив1;массив2).

Для вычисления критического значения -статистики при построении доверительного интервала для коэффициента корреляции используется функция Excel (Приложение 1):

СТЬЮДРАСПОБР(вероятность;степени_свободы).

3. Регрессия.Наряду с корреляционным анализом проводится регрессионный анализ, который заключается в определении формы связи зависимой случайной величины  с независимыми случайными величинами , , …,.

Форма связи результативного признака  с факторами , , …, называется уравнением регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (квадратичная, экспоненциальная, логарифмическая и т. д.).

В зависимости от числа взаимосвязанных признаков различают парную и множественную регрессии. Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной, если между тремя и более признаками – множественной (многофакторной) регрессией.

При изучении регрессии следует придерживаться определенной последовательности этапов.

Этап 1. Установление формы зависимости. Пусть в результате наблюдений двумерной случайной величины  получены данные, представляющие собой совокупность точек , , …, . Графическое изображение этих точек в плоскости  представляет собой корреляционное поле (диаграмму рассеяния). Диаграмма рассеяния позволяет произвести визуальный анализ эмпирических данных и графически определить вид функции регрессии . При  диаграмму рассеивания случайного вектора  достаточно сложно изобразить графически. В этом случае регрессионная зависимость имеет вид .

Этап 2. Определение вида уравнения регрессии и его параметров (коэффициентов). Пусть результативный признак  линейно зависит от факторов , , …,. В общем виде теоретическая линейная регрессия представима в виде

,

где , , …,  – неизвестные коэффициенты,  – случайные отклонения.

Для определения значений неизвестных коэффициентов необходимо знать и использовать все значения переменных , , …, и  генеральной совокупности, что практически невозможно. Поэтому по выборке ограниченного объема строится эмпирическое уравнение регрессии:

,

где  – теоретические значения результативного признака, полученные путем подстановки соответствующих значений факторных признаков в уравнение регрессии; , , …,  – оценки неизвестных коэффициентов уравнения регрессии.