Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 20

Пусть , , …,  – математические ожидания результативного признака  соответственно при уровнях , , …, . Если для различных групп фактора  математические ожидания не изменяются, то считается, что результативный признак  не зависит от фактора , в противном случае такая зависимость имеется.

Поскольку числовые значения математических ожиданий неизвестны, то возникает задача проверки гипотезы

:

в предположении выполнения следующих условий для каждой группы фактора:

1) наблюдения независимы и проводятся в одинаковых условиях,

2) результативный признак  имеет нормальный закон распределения с постоянной дисперсией для различных групп.

Поскольку числовые значения дисперсий различных групп неизвестны, то можно установить их равенство, проверив гипотезу о равенстве дисперсий : с помощью статистики Бартлетта [7]:

,

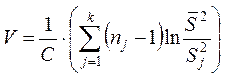имеющей распределение близкое к -распределению с  степенями свободы.

Здесь

,

,

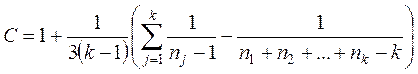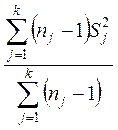 – выборочная дисперсия -ой группы ().

При заданном уровне значимости  находится критическая точка =, определяющая правостороннюю критическую область . По выборочным данным вычисляется наблюдаемое значение статистики . Если >, то гипотеза : отвергается, в противном случае принимается.

Если гипотеза : подтверждается, то можно приступать непосредственно к процедуре однофакторного дисперсионного анализа, т.е. проверке гипотезы :.

Общая сумма квадратов отклонений (общая вариация) отдельных наблюдений  от общей средней , вызванная влиянием на  фактора  и случайных неучтенных (остаточных) факторов, вычисляется по формуле

.

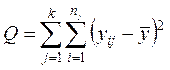Сумма  разлагается на сумму

+,

где = 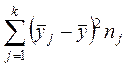– сумма квадратов отклонений между группами (межгрупповая вариация), вызванная влиянием фактора  на  и характеризующая рассеяние групповых средних около общей средней; = 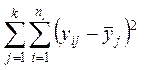– сумма квадратов отклонений внутри групп (остаточной вариации), вызванная влиянием на  остаточных факторов и характеризующая рассеяние отдельных наблюдений группы около ее средней.

По выборке значений результативного признака  находятся три несмещенные оценки 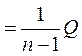, , 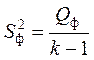 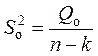дисперсии  случайной величины , причем  всегда является несмещенной оценкой, а ,  только при выполнении  гипотезы :, т.е. только в том случае, когда фактор  не влияет на результативный признак .

Проверка нулевой гипотезы  основывается на сравнении оценок , . Для этого используется статистика

=,

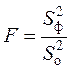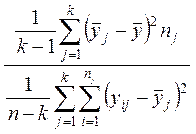имеющая -распределение с  и  степенями свободы.

По статистическим данным вычисляется наблюдаемое значение статистики . Для заданного уровня значимости  по таблицам критических точек -распределения находится критическая точка статистики = и строится правосторонняя критическая область . Если <, то нулевая гипотеза не отвергается, и в этом случае говорят, что влияние фактора  на признак  не подтвердилось выборочными наблюдениями.

Если в процессе анализа выявлено влияние фактора  на результативный признак , то степень данного влияния измеряется с помощью выборочного коэффициента детерминации

,

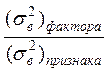показывающего какая доля вариации  объясняется зависимостью результативного признака  от влияющего фактора .

Работа в Excel. Для анализа данных с помощью Критерия Бартлетта используется статистические функции

ДИСП(число1;число2;…),

ХИ2ОБР(вероятность;степени_свободы).

Таблица 2. Однофакторный дисперсионный анализ: дисперсии групп

ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Столбец 1
Столбец 2
Столбец

Для проведения однофакторного анализа используется Однофакторный дисперсионный анализ из Анализа данных меню Сервис. После заполнения одноименного диалогового окна результат анализа появляется в виде двух таблиц. Формулы, по которым выполняются расчеты в Excel, представлены в таблицах 2 и 3 соответственно.