Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 15

Для двух случаев альтернативной гипотезы  при заданном уровне значимости , имеют место следующие критические точки статистики  и критические области.

При альтернативной гипотезе  по таблице критических точек распределения Фишера находится точка

.

Если , то нет оснований отвергнуть нулевую гипотезу; если , то нулевая гипотеза отвергается.

При альтернативной гипотезе , используя таблицы критических точек распределения Фишера, находится точки

, .

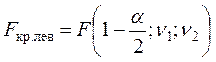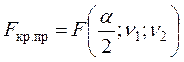Если , то нет оснований отвергнуть нулевую гипотезу; в противном случае нулевая гипотеза отвергается.

Работа в Excel.Для проверки данной гипотезы используем статистический анализ Двухвыборочный F-тест для дисперсии из Анализа данных меню Сервис (Приложение 2).

Результат анализа появится в виде таблицы. Формулы и соответствующие функции Excel, по которым выполняются расчеты в данном режиме, приводятся в таблице 5.

Данный режим рассчитывает только односторонние оценки -значения и , поскольку режим Двухвыборочный -тест для дисперсии при проверке гипотезы : в качестве альтернативной рассматривает  (если ), или  (если ). Чтобы получить двустороннюю оценку для  (в этом случае рассматривается альтернативная гипотеза ), используется функция

FРАСПОБР(вероятность;степени_свободы1;степени_свободы2).

Тогда значение левосторонней критической точки есть

=FРАСПОБР(),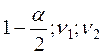

значение правосторонней критической точки –

=FРАСПОБР().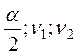

Двусторонняя критическая область есть объединение двух интервалов:

.

Двустороннее -значение рассчитывается с помощью функции

ФТЕСТ(массив1;массив2).

Таблица 5. Двухвыборочный F-тест для дисперсии

	Переменная 1		Переменная 2
Среднее	СРЗНАЧ		СРЗНАЧ
Дисперсия	ДИСП		ДИСП
Наблюдения	СЧЕТ		СЧЕТ
df	Число степеней свободы
F	Наблюдаемое значение F-статистики
P(F<=f) одностороннее	Если  (), то FРАСП(F; ;)  – число степеней большей исправленной дисперсии (= или =),  – число степеней меньшей исправленной дисперсии (= или =)
F критическое одностороннее	Критическое значение F-критерия определяется по таблицам распределения Фишера , FРАСПОБР(; ;)

Вопросы для самоконтроля

1  Что называется гипотезой?

2  Какая гипотеза называется: нулевой, альтернативной, простой и сложной?

3  Что называется критерием и мощностью критерия?

4  Что определяет уровень значимости гипотезы?

5  Что такое критическая область критерия?

6  Как найти доверительную вероятность статистического критерия?

7  Какие виды ошибок могут быть при проверке гипотез?

8  Что называется мощностью критерия?

9  В чем состоит смысл -значения?

10  Какие статистики используются при проверке гипотез о законе распределения?

11  Какие статистики используются при проверке гипотез о равенстве математических ожиданий двух нормальных выборок?

12  Какая статистика используется при проверке гипотезы о равенстве дисперсий нормальных выборок?

4. Лабораторная работа

Задание

Пусть случайная величина  характеризует расход сырья при производстве продукции по одной технологии,  – по другой, причем предполагается, что  и  нормально распределены. В результате наблюдений получены выборка  из генеральной совокупности случайной величины  и выборка  из генеральной совокупности случайной величины .

Выборка :

114	112	132	124	119	124	119	116	129	116
124	119	119	114	129	116	124	129	116	119
110	124	140	119	124	129	119	124	124	124
116	129	119	124	110	124	112	114	129	116
119	116	129	116	119	114	132	119	124	112