Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 22

По выборочным данным результативного признака  находятся четыре несмещенные оценки 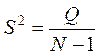, , 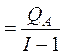,  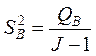(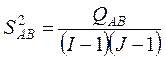, 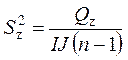) дисперсии  случайной величины , причем оценка  всегда является несмещенной оценкой, оценка  – при выполнении гипотезы : (когда фактор  не влияет на результативный признак ), оценка  – при выполнении гипотезы : (когда фактор  не влияет на результативный признак ),  при выполнении гипотез  и . Оценка  характеризует взаимодействие факторов  и .

Проверка гипотезы  () основывается на сравнении оценок  () и . Для этого используется статистика

 ,

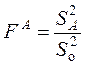
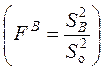имеющая -распределение с  () и  степенями свободы.

По статистическим данным вычисляется наблюдаемое значение статистики  (). Для заданного уровня значимости  по таблицам критических точек -распределения находится критическая точка статистики = (=) и строится правосторонняя критическая область  . Если < (<) то нулевая гипотеза не отвергается, и в этом случае говорят, что влияние фактора  () на признак  не подтвердилось выборочными наблюдениями.

Проверка гипотезы  основывается на сравнении оценок  и . Для этого используется статистика 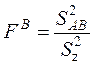, имеющая -распределение с  и  степенями свободы. По статистическим данным вычисляется наблюдаемое значение статистики . Для заданного уровня значимости  по таблицам критических точек -распределения находится критическая точка статистики = и строится правосторонняя критическая область . Если <,  то нулевая гипотеза не отвергается, и в этом случае говорят, что взаимное влияние факторов  и  на признак  не подтвердилось выборочными наблюдениями.

Двухфакторный дисперсионный анализ имеет две разновидности: без повторений () и с повторениями (). В первом случае каждому уровню фактора соответствует только одна выборка данных, во втором – определенным уровням факторов соответствует  выборок.

Работа в Excel. Для проведения двухфакторного анализа без повторений (или с повторениями) используется Двухфакторный дисперсионный анализ без повторений (или Двухфакторный дисперсионный анализ с повторениями) из Анализа  данных меню Сервис.

После заполнения диалогового окна Двухфакторный дисперсионный анализ без повторений результат анализа появляется в виде двух таблиц. Формулы, по которым выполняются расчеты в Excel, представлены в таблицах 5 и 6 соответственно.

Таблица 5. Двухфакторный дисперсионный анализ без повторений: дисперсии групп

ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Строка 1	СЧЕТ	СУММ	СРЗНАЧ	ДИСП
…	…	…	…
Строка I	СЧЕТ	СУММ	СРЗНАЧ	ДИСП
Столбец 1	СЧЕТ	СУММ	СРЗНАЧ	ДИСП
Столбец J	СЧЕТ	СУММ	СРЗНАЧ	ДИСП

Таблица 6. Двухфакторный дисперсионный анализ без повторений: расчет параметров для проверки гипотезы

Дисперсионный анализ
Источник вариации	Строки	Столбцы	Погрешность	ИТОГО
SS	= =	= =	= =	=
df
MS
F	= =	= =
P-Значение	FРАСП	FРАСП
Значимость F	= FРАСПОБР	= FРАСПОБР

Замечание. В Excel на экран выводится таблица, строки которой записаны в столбцах таблицы 6.

После заполнения диалогового окна Двухфакторный дисперсионный анализ с повторениями результат анализа появляется в виде двух таблиц. Формулы, по которым выполняются расчеты в Excel, представлены в таблицах 7 и 8 соответственно.