ДОВЕРИТ(альфа;станд_откл;размер),
которая
рассчитывает предельную точность оценки 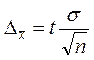 . Параметры
этой функции могут быть взяты из результата анализа Описательная статистика.
. Параметры
этой функции могут быть взяты из результата анализа Описательная статистика.
Доверительный интервал для
математического ожидания ![]() при неизвестной дисперсии
при неизвестной дисперсии
![]() с
доверительной вероятностью
с
доверительной вероятностью ![]() имеет вид:
имеет вид:
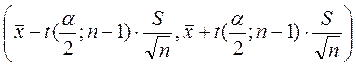 ,
,
где
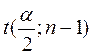 – критическая точка распределения
Стьюдента. Величина
– критическая точка распределения
Стьюдента. Величина 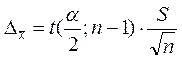 называется предельной ошибкой
выборочной средней. Здесь:
называется предельной ошибкой
выборочной средней. Здесь: 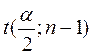 – квантиль распределения,
соответствующая уровню значимости
– квантиль распределения,
соответствующая уровню значимости ![]() : при
: при ![]() это квантиль нормального закона
распределения, при
это квантиль нормального закона
распределения, при ![]() – квантиль распределения
Стьюдента с
– квантиль распределения
Стьюдента с ![]() степенями свободы для двусторонней области;
степенями свободы для двусторонней области;
![]() – стандартное отклонение;
– стандартное отклонение; ![]() – объем выборки.
– объем выборки.
Работа в Excel. Для построения доверительного интервала математического ожидания при неизвестной дисперсии используется статистическая функция (приложение 1)
СТЬЮДРАСПОБР(вероятность;степени_свободы)
которая
рассчитывает значение 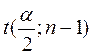 .
.
Доверительный интервал для
дисперсии ![]() при известном математическом ожидании
при известном математическом ожидании ![]() имеет вид
имеет вид
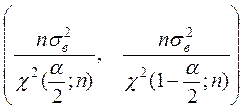 ,
,
где 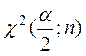 ,
, 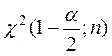 –
критические точки
–
критические точки ![]() распределения.
распределения.
Доверительный интервал для
дисперсии ![]() с неизвестным математическим ожиданием
с неизвестным математическим ожиданием![]() имеет вид
имеет вид
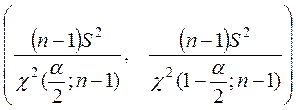 .
.
Здесь
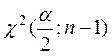 ,
, 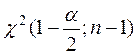 –
критические точки
–
критические точки ![]() распределения.
распределения.
Работа в Excel. Для построения доверительных интервалов для дисперсии используется статистическая функция (приложение 1)
ХИ2ОБР(вероятность;степени_свободы).
Вопросы для самоконтроля
1 Какие числовые характеристики выборки относятся к показателям положения?
2 Какие числовые характеристики выборки относятся к показателям разброса?
3 Какой показатель характеризует симметрию распределения?
4 Что называется выборочным средним, модой, медианой, выборочной дисперсией?
5 Каким условиям должны удовлетворять точечные оценки?
6 В чем суть метода моментов?
7 В чем суть метода максимального правдоподобия?
8 Какая функция называется функцией правдоподобия?
9 Какие оценки называются интервальными?
10 Что называется доверительной вероятностью?
4. Лабораторная работа
Задание
В результате наблюдений получена выборка ![]() из генеральной совокупности случайной
величины
из генеральной совокупности случайной
величины ![]() , характеризующей расход сырья при
производстве продукции по данной технологии:
, характеризующей расход сырья при
производстве продукции по данной технологии:
|
114 |
112 |
132 |
124 |
119 |
124 |
119 |
116 |
129 |
116 |
|
124 |
119 |
119 |
114 |
129 |
116 |
124 |
129 |
116 |
119 |
|
110 |
124 |
140 |
119 |
124 |
129 |
119 |
124 |
124 |
124 |
|
116 |
129 |
119 |
124 |
110 |
124 |
112 |
114 |
129 |
116 |
|
119 |
116 |
129 |
116 |
119 |
114 |
132 |
119 |
124 |
112 |
Требуется:
1) определить числовые характеристики выборки;
2) предполагая, что случайная величина ![]() имеет нормальное распределение
имеет нормальное распределение
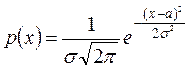 ,
,
методами
моментов и максимального правдоподобия оценить неизвестные параметры ![]() и
и ![]() ;
;
3) найти доверительные интервалы для математического
ожидания и дисперсии при уровне надежности 95%, считая, что ![]() имеет нормальное распределение.
имеет нормальное распределение.
Порядок выполнения работы
1. Числовые характеристики выборки. Для вычисления числовых характеристик выборки используется анализ Описательная статистика из Анализа данных меню Сервис (приложение 2). Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис. 1):
·
Входной интервал – вводятся ссылки на ячейки А1:А51, в которых
находятся значения выборки ![]() ;
;
· Группирование(по столбцам, по строкам)– по столбцам;
· Метки в первой строке (метки в первом столбце) – проставляется флажок;
· Выходной диапазон – вводится ссылка на новый рабочий лист «Опис_стат»;
· устанавливаются флажки Итоговая статистика, Уровень надежности (95%), К-ый наибольший, К-ый наименьший.
В указанном выходном диапазоне получится результат анализа Описательная статистика, приведенный на рисунке 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.