Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 21

Таблица 3. Однофакторный дисперсионный анализ: расчет параметров для проверки гипотезы

Дисперсионный анализ
Источник вариации	Между группами	Внутри групп	Итого
	=	=	+
P-Значение	FРАСП
Значимость	FРАСПОБР

Замечание. В Excel на экран выводится таблица, строки которой записаны в столбцах таблицы 3.

3. Двухфакторный дисперсионный анализ. Дисперсионный анализ рассматривает влияние двух независимых факторов  и  на изменчивость результативного признака . Пусть фактор  имеет  уровней , , …, , фактор  –  уровней , , …, , а число всевозможных сочетаний уровней этих факторов – . На каждом сочетании  и , , , имеется  выборочных значений результативного признака . Поэтому общее число наблюдаемых значений признака  равно . Результаты наблюдений и групповые средние (описанные ниже) могут быть представлены в виде таблицы 4.

Таблица 4. Результаты наблюдений для двухфакторного анализа

		Уровни (группы) фактора				Групповые средние уровней фактора A
				…
Уровни (группы) фактора A				…
		…	…	…	…
				…
				…
		…	…	…	…
				…
	…	…	…	…	…	…
				…
		…	…	…	…
				…
Групповые средние уровней фактора B				…

Пусть  – математическое ожидание результативного признака  на уровне , ,  – математическое ожидание результативного признака  на уровне , ,  – математическое ожидание результативного признака  на сочетании уровней  и , , . Если при изменении уровня фактора  групповые математические ожидания не изменяются, т.е. , то считается, что результативный признак  не зависит от фактора , в противном случае такая зависимость имеется. Аналогично, если при изменении уровня фактора  сохраняется равенство , то считается, что  не зависит от фактора . Если , то считается, что результативный признак  не зависит от взаимодействия факторов  и . Поскольку числовые значения математических ожиданий неизвестны, то возникает задача проверки следующих гипотез:

:   ,

:   ,

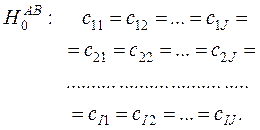
Проверка этих гипотез, также как и в задаче однофакторного дисперсионного анализа, возможна только при выполнении следующих условий:

1) при различных сочетаниях уровней факторов  и  наблюдения независимы и проводятся в одинаковых условиях,

2) при каждом сочетании уровней  и , , , результативный признак  имеет нормальный закон распределения с постоянной для различных сочетаний генеральной дисперсией .

Источниками изменчивости признака  являются фактор , фактор , взаимодействие факторов  и , а также  влияние неучтенных случайных (остаточных) факторов.

Общая сумма квадратов отклонений (общая вариация) отдельных наблюдений  от общей средней , вызванная влиянием на признак  факторов  и , а также остаточных факторов, вычисляется по формуле

.

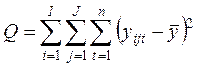Сумма  равна

++,

где 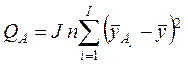,  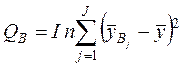– суммы квадратов отклонений вызванных влиянием соответственно факторов  и  на ; =+ – сумма квадратов отклонений, вызванная влиянием на  одновременным взаимодействием факторов  и , а также остаточных факторов,

, .

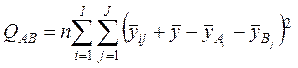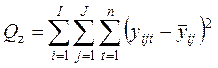В приведенных формулах 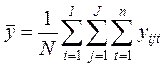 – общая средняя, 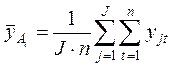 – средние значения признака  на уровнях фактора  (по строкам), 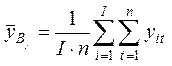 – средние значения признака  на уровнях фактора  (по столбцам), 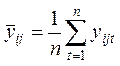 – средние значения признака  при различных сочетаниях уровней  и , , .