Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 17

·  в ячейки B2:B9 копируется столбец Интегральный процент. После этого необходимо изменить числовой формат в данных ячейках с процента на число с помощью команды Формат-Ячейки…-Число-Числовой-ОК;

·  в ячейки B10, B11 и B12 копируются значения Среднее, Стандартное отклонение  и Счет из Описательной статистки;

·  ячейки С2:С9 содержат формулу

{=НОРМРАСП(А2:А9;В10;В11;ИСТИНА)};

·  ячейки D2:D9 содержат формулу

{=ABS(B2:B9-C2:C9)};

·  ячейка B13 содержит формулу

=МАКС(D2:D9);

·  ячейка В14 содержит формулу

=В13*КОРЕНЬ(В12).

Вывод. Поскольку , то нет оснований для отклонения нулевой гипотезы о нормальном законе расхода сырья при производстве продукции.

2. Проверка гипотезы о равенстве математических ожиданий при известных и равных дисперсиях.По выборкам  и  значений нормально распределенных случайных величин ~ и ~ выдвигается гипотеза о равенстве математических ожиданий:

:,

в предположении, что  и  известны и равны, при альтернативной гипотезе , которая может быть одной из следующих:

1) , ,

2) ,

3) .

Для проверки данной гипотезы используется режим анализа Двухвыборочный -тест для средних. Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис. 3):

·  Интервал переменной 1 – вводятся ссылки на ячейки А1:А51, в которых находятся название и значения выборки ;

·  Интервал переменной 2 – вводятся ссылки на ячейки C1:C61, в которых находятся название и значения выборки ;

·  Гипотетическая средняя разность – вводится число 0 (нуль);

·  Дисперсия переменной 1 (известная) – вводится предварительно вычисленное с помощью функции

ДИСП(число1;число2;…)

значение несмещенной выборочной дисперсии , которая является оценкой дисперсии  генеральной совокупности случайной величины ;

·  Дисперсия переменной 2 (известная) – вводится предварительно вычисленное с помощью функции ДИСП значение выборочной дисперсии , которая является оценкой дисперсии  генеральной совокупности случайной величины ;

·  Метки – устанавливается флажок;

·  Альфа – вводится уровень значимости 0,05;

·  Выходной диапазон– вводится ссылка на новый рабочий лист «z-тест».

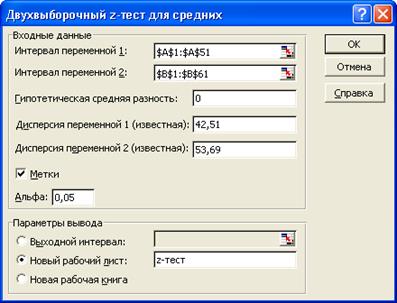
Рис. 3. Заполнение диалогового окна

Двухвыборочный -тест для средних

Рассчитанные в данном режиме показатели представлены на рисунке 4.

Вывод. Так как наблюдаемое значение  попадает в область допустимых значений, т.е. 1,0119==1,9599, то нет оснований отвергнуть нулевую гипотезу : на уровне значимости 0,05 при альтернативной гипотезе , . Для -значения имеет место неравенство 0,3116>0,05, что также говорит о хорошем согласии с .

Следовательно, средний расход сырья для производства продукции по разным технологиям совпадает в 95% случаев наблюдений, и только в 5% случаев различается.

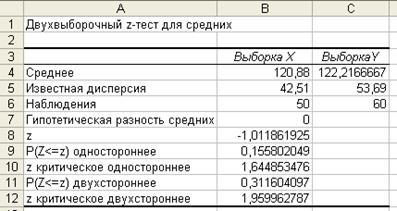
Рис. 4. Результаты проверки гипотезы ,

где  и  известны и

При альтернативной гипотезе  () имеют место неравенства:

=1,0119<1,6448=, =0,1558>0,05,

значит, гипотеза  принимается при заданном уровне значимости =0,05. Следовательно, различие средних расходов сырья по двум разным технологиям незначимо.

3. Проверка гипотезы о равенстве математических ожиданий при неизвестных и равных дисперсиях (малые независимые выборки).По выборкам  и  значений нормально распределенных случайных величин ~ и ~ выдвигается гипотеза о равенстве математических ожиданий:

:,

в предположении, что  и  неизвестны и равны, при альтернативной гипотезе , которая может быть одной из следующих гипотез:

1) , ,

2) ,

3) .

Для проверки данной гипотезы используется режим анализа Двухвыборочный -тест с одинаковыми дисперсиями. Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис. 5):

·  Интервал переменной 1 – вводятся ссылки на ячейки А1:А51, в которых находятся значения выборки ;

·  Интервал переменной 2 – вводятся ссылки на ячейки В1:В61, в которых находятся значения выборки ;

·  Гипотетическая средняя разность – вводится число 0;

·  Метки – устанавливается флажок;