Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 3

3. Что называется статистической функцией распределения?

4. Какими свойствами обладает статистическая функция распределения?

4. Лабораторная работа

Задание

В результате наблюдений получена выборка  из генеральной совокупности случайной величины , характеризующей расход сырья при производстве продукции по данной технологии:

114	112	132	124	119	124	119	116	129	116
124	119	119	114	129	116	124	129	116	119
110	124	140	119	124	129	119	124	124	124
116	129	119	124	110	124	112	114	129	116
119	116	129	116	119	114	132	119	124	112

Требуется:

1) построить вариационный ряд и полигон относительных частот;

2) построить интервальный ряд, гистограмму, кумулятивную кривую.

Порядок выполнения работы

1. Вариационный ряд, полигон частот. В ячейку A1 вводится название «Выборка », а ячейки А2:А51 – значения выборки . Для построения вариационного ряда выполняются следующие действия:

– выделяются ячейки А2:А51, выделенный массив сохраняется в ячейках B2:B51 и активизируется на панели инструментов кнопка Сортировка по возрастанию  (отсортированная выборка располагается в тех же ячейках столбца B);

– в ячейки столбца С копируются неповторяющиеся варианты выборки, в соответствующих ячейках столбца D вводятся частоты вариант;

– в ячейки столбца Е вводится формула

{=D2:D10/50}

для подсчета относительных частот вариант.

Полученный вариационный ряд представляет собой таблицу, расположенную в столбцах C, D, E (рис. 2).

Для построения полигона частот выполняются следующие действия:

– на панели инструментов активизируется кнопка Мастер диаграмм (шаг 1 из 4), в одноименном диалоговом окне среди стандартных типов выбирается График и верхний левый вид диаграммы и нажимается кнопка Далее>;

– открывается диалоговое окно Мастер диаграмм (шаг 2 из 4), в котором во вкладке Диапазон данных в поле Диапазон вводится ссылка на диапазон частот D2:D34; во вкладке Ряд в поле Подписи оси Х вводится ссылка на массив вариант С2:С34, в поле Имя – название «Полигон частот»; нажимается кнопка Далее>,

– открывается диалоговое окно Мастер диаграмм (шаг 3 из 4), в котором во вкладке Заголовки в поле Ось Х(категорий) вводится название «Варианты», в поле Ось Y(значений) – название «Частоты»; во вкладке Легенда снимается флажок Добавить легенду и нажимается кнопка Далее>;

– открывается диалоговое окно Мастер диаграмм (шаг 4 из 4) в поле имеющемся устанавливается флажок.

Построенный полигон частот изображен на рисунке 2.

Вывод. По виду полигона частот можно предположить, что случайная величина  расхода сырья при производстве продукции по данной технологии имеет нормальное распределение.

Замечание. На графике полигона частот по оси вариант не выдержан масштаб, что не мешает правильно оценить характер распределения исследуемого признака.

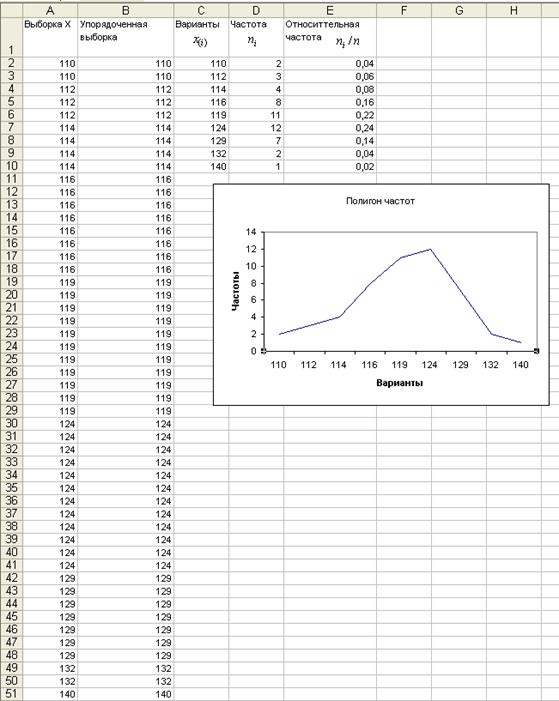
Рис. 2. Вариационный ряд и полигон частот

2. Интервальный ряд, гистограмма, кумулятивная кривая. Для построения интервального ряда выборки  используется анализ Гистограмма из Анализа данных меню Сервис. Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис. 3):

·  Входной интервал – вводятся ссылки на ячейки А1:А51, в которых находятся значения выборки ;

·  Интервал карманов – не заполняется;

·  Метки – устанавливается флажок;

·  Выходной диапазон– вводится ссылка на новый рабочий лист «Гистограмма».

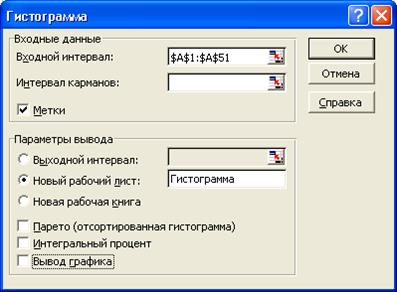
Рис. 3. Заполнение диалогового окна

Гистограмма

Результаты вычислений появляются в виде таблицы (рис. 4), которая является интервальным рядом.

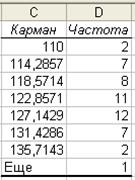
Рис. 4. Интервальный ряд