Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 19

Для определения двусторонней критической области выполняются следующие действия:

·  в ячейку В11 вводится формула

=FРАСПОБР(1-0,025;49;59);

·  в ячейку В12 вводится формула

=FРАСПОБР(0,025;49;59);

·  в ячейку В13 вводится формула

=ФТЕСТ(А2:А51;С2:С61),

где А2:А51 и С2:С61 ссылки на ячейки, содержащие значения выборок  и  соответственно.

Вывод. Наблюдаемое значение  попадает в область допустимых значений, 0,7918==0,6318. Поэтому нет оснований отвергнуть нулевую гипотезу : о равенстве дисперсий расхода сырья по двум технологиям на уровне значимости 0,05 при альтернативной гипотезе  (если ), или  (если ). Для -значения имеет место неравенство 0,2>0,05, что также говорит о хорошем согласии с .

При альтернативной гипотезе  имеем:

0,7918=(0,5779;1,7069) и =0,4021>0,05,

значит, гипотеза : также принимается на уровне значимости =0,05.

Тема 4

ДИСПЕРСИОННЫЙ АНАЛИЗ

1  Дисперсионный анализ

2  Однофакторный дисперсионный анализ

3  Двухфакторный дисперсионный анализ

4  Лабораторная работа

Изучение реальных процессов предполагает получение не только прогнозной оценки исследуемого показателя, но и количественной характеристики степени влияния на него различных факторов, а также оценки возможных последствий их изменений в будущем. В результате опыта проводятся наблюдения над целым рядом случайных величин. При этом возникает задача изучения взаимосвязи между случайными величинами, которая решается в три этапа:

– проводится оценка существенности влияния одного фактора на другой с помощью дисперсионного анализа;

– проводится численная оценка связи с помощью корреляционного анализа;

– строятся функциональные зависимости посредством регрессионного анализа.

1. Дисперсионный анализ. Дисперсионный анализ служит для статистического установления влияния отдельных факторов на изменчивость какого-либо признака, значения которого могут быть получены опытным путем в виде выборки из генеральной совокупности случайной величины . Под факторами понимаются различные независимые показатели, количество которых может быть различным. Конкретная реализация фактора  называется уровнем (группой) этого фактора. В зависимости от количества факторов различают однофакторный и многофакторный дисперсионный анализ. Величина  называется результативным признаком (фактором) . Идея дисперсионного анализа состоит в том, что дисперсия признака  разлагается на сумму дисперсий, вызванных влиянием факторов, дисперсий, вызванных взаимодействием факторов и случайной дисперсии, вызванной неучтенными случайными факторами. Затем указанные дисперсии сравниваются.

2. Однофакторный дисперсионный анализ. Однофакторный дисперсионный анализ позволяет статистически обосновать степень влияния на результативный признак  одного фактора  для различных уровней или групп , , …, , например, установление зависимости выполненных на стройке за смену работ (признак ) от работающей бригады (группы , , …, ). В таблице 1 представлены выборочные значения результирующего признака  для различных групп.

Таблица 1. Данные наблюдений для однофакторного дисперсионного анализа

Номера наблюдений	Уровни (группы) фактора
			…
1			…
2			…
…	…	…	…	…
			…
Групповая средняя			…

Здесь , , …,  – численность наблюдений в уровнях , , …,  соответственно, при этом  .

Из таблицы находятся групповые средние

, ,

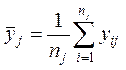и общая средняя

=.

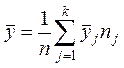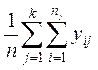Изменчивость значений  от одного уровня к другому объясняется влиянием фактора  на результативный признак , а изменчивость тех же значений в пределах одного уровня характеризуется влиянием неучтенных случайных (остаточных) факторов.