Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 12

Гипотезы о законе распределения исследуемой случайной величины . Проверка гипотезы о законе распределения осуществляется с помощью критериев согласия, основанных на выборе определенной меры (т.е. критерия) расхождения между теоретическим и эмпирическим распределениями. Если такая мера расхождения для рассматриваемого случая попадает в критическую область, то гипотеза отвергается, в противном случае принимается.

Критерий согласия Пирсона . Пусть генеральная совокупность значений случайной величины  имеет неизвестное распределение. На основании выборки  выдвигается гипотеза  о конкретном законе распределения  (нормальном, биномиальном, показательном и т.д.), выраженном через функцию распределения . Это распределение называется теоретическим. По выборке  находится эмпирическая функция распределения . Необходимо проверить гипотезу

при альтернативной гипотезе [2]:

.

В критериях согласия иногда альтернативная гипотеза не указывается.

Для проверки данной гипотезы статистика

=,

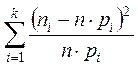имеющая распределение  с  степенями свободы. Здесь  – число параметров распределения , которые оцениваются по выборке ;  – объем выборки;  – число непересекающихся интервалов выборочных значений

, , , ,

, , , ;  – число значений выборки, принадлежащих интервалу , ;  – вероятности попадания значений случайной величины в каждый из этих интервалов:

, ,

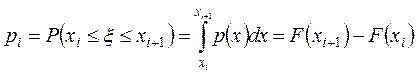 – плотность распределения вероятностей случайной величины , . Если в некоторых интервалах условие  не выполняется, то эти интервалы объединяются с соседними.

По выборке  вычисляется наблюдаемое значение  статистики. Для выбранного уровня значимости  по таблице распределения  находится число .

Вывод. Гипотеза  не противоречит выборке наблюдений на заданном уровне значимости, если  ; если же , то гипотеза  отвергается.

Работа в Excel. Для вычисления наблюдаемого и критического значений статистики  используются следующие функции Excel (Приложение 1):

НОРМРАСПР(; среднее; стандартное_откл; интегральная),

ХИ2РАСП(вероятность; степени_свободы).

Критерий согласия Колмогорова. Данный критерий основывается на мере  отклонения эмпирической функции распределения  выборки  от теоретической функции распределения  случайной величины . Он применяется в случае, когда гипотетически (по предположению) известны закон распределения  и все его параметры, а на основании опытных данных необходимо подтверждение его справедливости.

По выборке  из генеральной совокупности случайной величины  с неизвестной функцией распределения  выдвигается гипотеза:

.

Для проверки данной гипотезы используется статистика

=.

Здесь величина  является случайной величиной, имеющей распределение Колмогорова и характеризующей максимальное отклонение эмпирической функции распределения  от теоретической ;  – объем выборки.

По выборке  вычисляется наблюдаемое значение  статистики. Задавая уровень значимости , по таблице значений функции Колмогорова (Приложение 3) определяется критическое значение статистики .

Вывод. Если , то нулевая гипотеза принимается, т.е. считается, что теоретическая функция распределения  согласуется с наблюденными данными, если , то  отклоняется.

Работа в Excel. Для вычисления наблюдаемого и критического значений статистики  используются следующие функции Excel:

НОРМРАСПР(; среднее; стандартное_откл; интегральная),

МАКС(число1;число2; ...),

ABS(число).

Гипотезы об однородности двух выборок. Пусть  и  нормально распределенные случайные величины, ~ и ~. И пусть  – выборка значений случайной величины , а  – выборка значений случайной величины . Необходимо по данным выборкам проверить равенства (однородность) математических ожиданий  и дисперсий .

Проверка гипотезы о равенстве математических ожиданий при известных и равных дисперсиях (большие независимые выборки).Будем считать, что дисперсии  и  известны и . Выдвигается гипотеза о равенстве математических ожиданий:

:,

причем  и  известны и равны.

Альтернативной гипотезой  может быть одна из следующих гипотез:

1) , ,

2) ,

3) .