Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 6

Рис. 2. Положительный (а) и отрицательный (б)

эксцессы распределения.

Работа в Excel. Для вычисления числовых характеристик выборки используется режим Описательная статистика из Анализа данных меню Сервис (приложение 2). Результат анализа представлен в виде таблицы. Формулы и функции Excel, по которым рассчитываются соответствующие числовые характеристики, приводятся в таблице 2.

Таблица 2. Описательная статистика

Среднее	СРЗНАЧ
Стандартная ошибка1
Медиана	МЕДИАНА
Мода	. Если выборка не содержит одинаковых вариант, то возвращается значение ошибки #Н/Д МОДА
Стандартное2 отклонение	СТАНДОТК
Дисперсия выборки	Несмещенная выборочная дисперсия2 ДИСП
Эксцесс	ЭКСЦЕСС
Асимметричность	СКОС
Интервал	Размах вариаций
Минимум	Наименьшее значение выборки МИН
Максимум	Наибольшее выборки МАКС
Сумма	СУММ
Счет	Объем выборки СЧЕТ
Наибольший(k)	Наибольшее значение в множестве данных, начиная с НАИБОЛЬШИЙ
Наименьший(k)	Наименьшее значение в множестве данных, начиная с НАИМЕНЬШИЙ
Уровень надежности3	Предельная ошибка средней выборочной ДОВЕРИТ

1 – 2 определены в пункте 2, а 3 – в пункте 3 данной темы

2. Точечные оценки параметров распределения. Пусть случайный эксперимент описывается случайной величиной . Повторяя случайный эксперимент  раз, получаем последовательность наблюденных значений  – выборка объема  из генеральной совокупности случайной величины .

Статистической оценкой параметра  называется приближенное значение параметра, полученное на основе статистических (выборочных) данных

,

где  – выборочная характеристика, вычисляемая по результатам  наблюдений величины , используемая в качестве оценки -характеристики генеральной совокупности. В качестве  могут быть параметры , параметр распределения и т. д.

По статистическим данным нельзя получить точную оценку неизвестного параметра , но можно найти приближенную оценку. Более того, каждая выборка объема  из генеральной совокупности дает свою оценку одного и того же неизвестного параметра , т.е. для  можно получить бесконечное множество его оценок. Поэтому оценку  можно считать случайной величиной, а ее значение , вычисленное по одной данной выборке можно рассматривать как одно из ее возможных значений.

Различают точечные и интервальные оценки.

Точечная оценка параметра  определяется одним числом . Качество оценки  устанавливается по следующим трем свойствам.

Несмещенность. Оценка  неизвестного параметра  генеральной совокупности называется несмещенной, если для фиксированного числа наблюдений  выполняется равенство: .

Состоятельность. Оценка , найденная по выборке объема , называется состоятельной, если для любого  выполняется равенство

,

которое означает, что при увеличении объема  выборки значение  сходится по вероятности к неизвестному параметру .

Эффективность. Несмещенная оценка  неизвестного параметра  называется эффективной, если среди всех подобных оценок того же параметра она имеет наименьшую дисперсию: .

Оценкой математического ожидания случайной величины  является ее выборочная средняя: 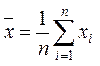. Она является несмещенной, состоятельной и эффективной.

Выборочная дисперсия 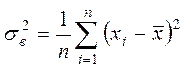 является смещенной оценкой для дисперсии случайной величины .

Величина

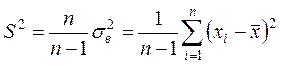
является несмещенной, эффективной и состоятельной оценкой дисперсии случайной величины  и называется несмещенной выборочной дисперсией, а смещенная дисперсия – генеральной дисперсией или дисперсией генеральной совокупности.

Величина  называется стандартным отклонением.

Стандартная ошибка выборки определяется по формуле .

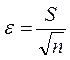Методы получения точечных оценок. Наиболее распространенными методами являются метод моментов и метод максимального правдоподобия.