Проверка нулевой гипотезы осуществляется с помощью ![]() -статистики
-статистики
![]() =
=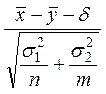 ,
,
имеющей стандартное нормальное распределение, ![]() ~
~![]() ;
;
![]() ,
, ![]() –
объемы выборок
–
объемы выборок ![]() и
и ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() –
выборочные средние и известные дисперсии выборок
–
выборочные средние и известные дисперсии выборок ![]() и
и ![]() соответственно;
соответственно; ![]()
![]() . В качестве оценок дисперсий
. В качестве оценок дисперсий ![]() ,
, ![]() в
реальных ситуациях при больших объемах выборок
в
реальных ситуациях при больших объемах выборок ![]() и
и ![]() используются несмещенные выборочные
дисперсии
используются несмещенные выборочные
дисперсии ![]() ,
, ![]() [14].
[14].
Вычисляется наблюдаемое значение ![]() данной статистики.
данной статистики.
Для трех случаев альтернативной гипотезы ![]() при заданном уровне значимости
при заданном уровне значимости ![]() , имеют место следующие критические точки
, имеют место следующие критические точки ![]() и критические области статистики
и критические области статистики ![]() .
.
При альтернативной гипотезе ![]() ,
,
![]() , используя таблицы функции Лапласа
, используя таблицы функции Лапласа ![]() ,
, ![]() =
=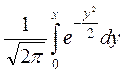 , находится
, находится ![]() из равенства
из равенства
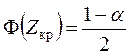 .
.
Если
![]()
![]()
![]() , то нет оснований отвергнуть нулевую гипотезу; при
, то нет оснований отвергнуть нулевую гипотезу; при ![]()
![]()
![]() нулевая гипотеза отвергается.
нулевая гипотеза отвергается.
При альтернативной гипотезе ![]() точка
точка
![]() определяется по таблице функции Лапласа из равенства
определяется по таблице функции Лапласа из равенства
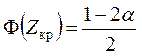 .
.
Если
![]()
![]()
![]() , то нет оснований отвергнуть нулевую гипотезу, при
, то нет оснований отвергнуть нулевую гипотезу, при ![]()
![]()
![]() нулевая гипотеза отвергается.
нулевая гипотеза отвергается.
При альтернативной гипотезе ![]() точка
точка
![]() определяется по таблице функции Лапласа также из равенства
определяется по таблице функции Лапласа также из равенства
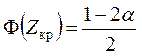 .
.
Если
![]()
![]() –
–![]() , то нет оснований отвергнуть нулевую гипотезу, а при
, то нет оснований отвергнуть нулевую гипотезу, а при ![]()
![]() –
–![]() нулевая гипотеза отвергается.
нулевая гипотеза отвергается.
Работа в Excel. Для проверки
данной гипотезы используется Двухвыборочный ![]() -тест
для средних из пакета Анализ данных меню Сервис
(приложение 2). Результат анализа появится в виде таблицы. Формулы и соответствующие
функции Excel, по которым выполняются расчеты в данном режиме,
приводятся в таблице 2.
-тест
для средних из пакета Анализ данных меню Сервис
(приложение 2). Результат анализа появится в виде таблицы. Формулы и соответствующие
функции Excel, по которым выполняются расчеты в данном режиме,
приводятся в таблице 2.
Проверка гипотезы о равенстве математических ожиданий
при неизвестных и равных дисперсиях (малые независимые выборки). Будем
считать, что дисперсии ![]() и
и ![]() неизвестны
и равны. Выдвигается гипотеза:
неизвестны
и равны. Выдвигается гипотеза:
![]() :
:![]() .
.
Альтернативной ![]() может
быть одна и следующих гипотез:
может
быть одна и следующих гипотез:
1)
![]() ,
, ![]() ,
,
2)
![]() ,
,
3)
![]() .
.
Проверка нулевой гипотезы осуществляется с помощью ![]() -статистики
-статистики
![]()
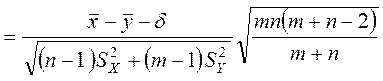 ,
,
имеющей распределение Стьюдента с ![]() степенями
свободы;
степенями
свободы; ![]() ,
, ![]() – объемы выборок
– объемы выборок ![]() и
и
![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() – выборочные средние и исправленные
дисперсии соответственно.
– выборочные средние и исправленные
дисперсии соответственно.
Вычисляется наблюдаемое значение ![]() статистики
статистики ![]() .
.
Таблица 2. Двухвыборочный ![]() -тест с одинаковыми дисперсиями
-тест с одинаковыми дисперсиями
|
Переменная 1 |
Переменная 2 |
|
|
Среднее |
СРЗНАЧ |
СРЗНАЧ |
|
Дисперсия |
ДИСП |
ДИСП |
|
Наблюдения |
СЧЕТ |
СЧЕТ |
|
Гипотетическая разность средних |
Число,
равное предполагаемой разности математических ожиданий |
|
|
|
Наблюдаемое
значение статистики
|
|
|
|
Если Если 1-НОРМРАСП( |
|
|
|
Модуль значений критических точек
НОРМСТОБР( |
|
|
|
Если 2*(1-НОРМРАСП( |
|
|
|
Модуль значений критических точек
НОРМСТОБР( |
|
При альтернативной гипотезе ![]() ,
,
![]() , используя таблицы критических точек
распределения Стьюдента, находится точка
, используя таблицы критических точек
распределения Стьюдента, находится точка
![]() .
.
Если
![]()
![]()
![]() , то нет оснований отвергнуть нулевую гипотезу. Если
, то нет оснований отвергнуть нулевую гипотезу. Если ![]()
![]()
![]() , то нулевая гипотеза отвергается.
, то нулевая гипотеза отвергается.
При альтернативной гипотезе ![]() по
таблице критических точек распределения Стьюдента находится точка
по
таблице критических точек распределения Стьюдента находится точка
![]() .
.
Если
![]()
![]()
![]() , то нет оснований отвергнуть нулевую гипотезу; если
, то нет оснований отвергнуть нулевую гипотезу; если ![]()
![]()
![]() , то нулевая гипотеза отвергается.
, то нулевая гипотеза отвергается.
При альтернативной гипотезе ![]()
![]() –
–![]() .
.
Если
![]()
![]() –
–![]() ,
то нет оснований отвергнуть нулевую гипотезу, а при
,
то нет оснований отвергнуть нулевую гипотезу, а при ![]()
![]() –
–![]() нулевая гипотеза отвергается.
нулевая гипотеза отвергается.
Работа в Excel.Для проверки данной гипотезы используем статистический анализ Двухвыборочный t-тест с одинаковыми дисперсиями из Анализа данных меню Сервис (приложение 2).
В выбранном выходном диапазоне появится результат анализа в виде таблицы. В таблице 3 приводятся формулы из [4] и соответствующие функции Excel, по которым рассчитываются соответствующие значения.
Проверка гипотезы о равенстве математических ожиданий
при неизвестных и неравных дисперсиях.Будем считать, что дисперсии
![]() и
и ![]() неизвестны
и неравны. Выдвигается гипотеза:
неизвестны
и неравны. Выдвигается гипотеза:
![]() :
:![]() .
.
Альтернативной ![]() может
быть одна и следующих гипотез:
может
быть одна и следующих гипотез:
1)
![]() ,
, ![]() ,
,
2)
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.