Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 7

Пусть распределение генеральной совокупности зависит от  параметров. Согласно методу моментов  теоретических моментов приравниваются к соответствующим выборочным моментам. При этом получается система из  уравнений, решением которой являются оценки каждого из  параметров. Достоинством данного метода является его простая вычислительная реализация, недостаток состоит в том, что получаемые оценки являются смещенными и мало эффективными.

Метод максимального правдоподобия состоит в том, что для получения оценки неизвестного параметра  нужно найти такое значение , при котором вероятность реализации выборки  была бы максимальной. С этой целью строится функция правдоподобия , определяющая вероятность получения выборки , и находится точка максимума этой функции, которая является оценкой неизвестного параметра .

Функция правдоподобия непрерывной случайной величины  с плотностью вероятности  имеет вид:

.

Функция правдоподобия дискретной случайной величины , для которой распределение вероятности , зависит от параметра  имеет вид:

.

Если оцениваемых параметров несколько , то строится и исследуется на максимум функция правдоподобия вида .

Поскольку функции  и  достигают экстремумы при одних и тех же значениях , то для упрощения расчетов иногда пользуются логарифмической функцией правдоподобия.

Метод наибольшего правдоподобия дает состоятельные оценки. Недостаток метода заключается в том, что иногда оценки наибольшего правдоподобия являются смещенными.

3. Интервальные оценки неизвестных параметров. Более полный и надежный способ оценивания параметров распределений заключается в определении не единственного точечного значения, а интервала, который с заданной вероятностью накрывает истинное значение оцениваемого параметра. Для заранее выбранного уровня значимости , , по выборке определяются два числа  и , , между которыми с вероятностью  находится неизвестный параметр :

.

Число  называется доверительной вероятностью (надежностью), ,  – доверительными нижней и верхней границами. Величины , определяются по результатам выборки, следовательно, являются случайными.

Если  – точечная оценка неизвестного параметра , то

,

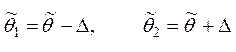где  – предельная ошибка (уровень надежности) выборки, которая либо задается заранее, либо вычисляется.

На практике часто используются односторонние доверительные интервалы, которые определяются из условий:

 или

и называются правосторонними и левосторонними соответственно.

Длина доверительного интервала, характеризующая точность интервальной оценки, зависит от объема выборки  и надежности . При увеличении  длина доверительного интервала уменьшается, а с приближением надежности к 1 – увеличивается. В качестве  принимают значения 0,9; 0,95; 0,99, что соответствует 90-, 95-, 99%-ым доверительным интервалам соответственно.

Задача определения доверительного интервала может быть решена только тогда, когда удается найти закон распределения случайной величины, используемой в качестве оценки, то есть плотность вероятности . В общем случае этот закон зависит от самого неизвестного параметра. Однако иногда удается перейти от оценки  к таким функциям выборочных значений, закон распределения которых зависит только от объема выборки  и закона распределения случайной величины  и не зависит от неизвестных параметров.

Пусть выборка  произведена из генеральной совокупности значений нормально распределенной с параметрами  и  случайной величины , т.е. ~.

Доверительный интервал для математического ожидания  при известной дисперсии  с доверительной вероятностью имеет вид:

.

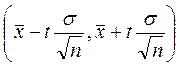Здесь 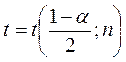 – квантиль порядка  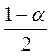нормального распределения, которое находится по таблицам интеграла вероятностей 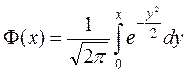,  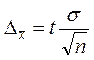– точность оценки. Из соотношения 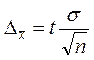 находится минимальный объем  выборки, который обеспечивает заданную точность :

.

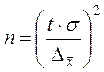Число , как правило, неизвестно, поэтому его заменяют приближенным значением: .

Работа в Excel. Для построения доверительного интервала математического ожидания при известной дисперсии используется статистическая функция (приложение 1)