Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 24

Содержимое ячеек таблицы:

·  в ячейках B2:F2 находятся объемы выборок , вычисленные с помощью функции СЧЕТ для каждого завода;

·  в ячейках B3:F3 находятся несмещенные оценки , вычисленные с помощью функции ДИСП для каждого завода;

·  в ячейки B4:F4 вводится формула

{=СУММПРОИЗВ(B2:F2-1;B3:F3)/СУММ(B2:F2-1)};

·  в ячейки B5:F5 вводится формула

{=1+1/(3*(5-1))*(СУММ(1/(B2:F2-1))-1/(СУММ(B2:F2)-5))};

·  в ячейки B6:F6 вводится формула

{=1/B5*СУММПРОИЗВ(B2:F2-1;LN(B4/B3:F3))},

рассчитывающая наблюдаемое значение  критерия Бартлетта;

·  ячейка B7 содержит формулу =ХИ2ОБР(0,05;5-1), определяющую критическую точку .

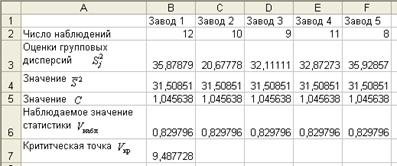
Рис. 4. Результаты проверки

гипотезы :

Так как =0,829796 не попадает в критическую область , то гипотеза о равенстве дисперсий групп принимается, поэтому можно приступить к проверке гипотезы о равенстве математических ожиданий.

              2. Однофакторный анализ – проверка нулевой гипотезы : (о равенстве средних значений объемов расходов пяти заводов). Для этого используется режим анализа Однофакторный дисперсионный анализ. Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис. 5):

·  Входной интервал – вводятся ссылки на ячейки А1:А51, в которых находятся наблюдаемые значения признака  и названия уровней фактора;

·  Группирование – проставляется автоматически;

·  Метки – устанавливается флажок;

·  Альфа – вводится уровень значимости 0,05;

·  Выходной диапазон– вводится ссылка на новый рабочий лист «Однофакт-анализ».

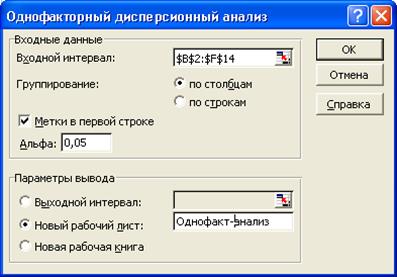
Рис. 5. Диалоговое окно

Однофакторный дисперсионный анализ

Показатели, рассчитанные в ходе анализа, представлены в виде двух таблиц «ИТОГИ» и «Дисперсионный анализ» на рисунке 6.

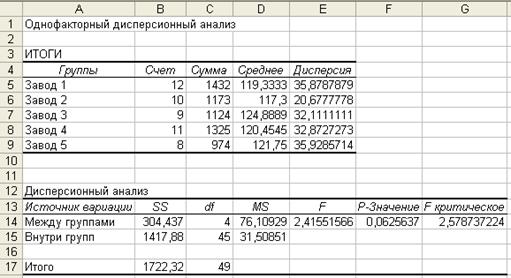
Рис. 6. Результат Однофакторного дисперсионного анализа

Вывод. Вычисленное значение =2,4155 не попадает в критическую область , поэтому нулевая гипотеза о равенстве математических ожиданий групп принимается. Следовательно, расход сырья статистически не зависит от завода, производящего продукцию. Для -значения имеет место неравенство 0,01<0,06, что также говорит о хорошем согласии гипотезы : с выборочными данными. С другой стороны, -значение находится близко к 0,05, что вызывает сомнения в ее истинности.

Выборочный коэффициент детерминации

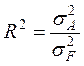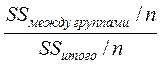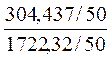===0,1768

показывает, что только 17% общей выборочной вариации расхода сырья связано с выбором завода.

              Задание 2.

              Результирующим признаком  является величина разрывной нагрузки пряжи, факторами – тип станка () и вид сырья () (см. рис. 2). Необходимо проверить гипотезы:

– о равенстве математических ожиданий групп фактора

:,

– о равенстве математических ожиданий групп фактора

:,

– о равенстве математических ожиданий взаимодействия факторов  и

:.

              Для решения данной задачи используется режим анализа Двухфакторный дисперсионный анализ без повторений. Значения параметров в одноименном диалоговом окне устанавливаются следующим образом (рис. 7):

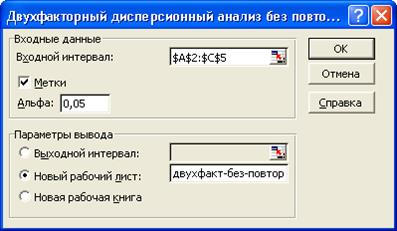
Рис. 7. Диалоговое окно Двухфакторный

 дисперсионный анализ без повторений

·  Входной интервал – вводятся ссылки на ячейки А2:C5, в которых находятся значения наблюдаемого признака  и названия уровней факторов;

·  Метки – устанавливается флажок;

·  Альфа – вводится уровень значимости 0,05;

·  Выходной диапазон– вводится ссылка на новый рабочий лист «Двухфакт-без-повторений».

Показатели, рассчитанные в ходе анализа, представлены в виде двух таблиц «ИТОГИ» и «Дисперсионный анализ» на рисунке 8.

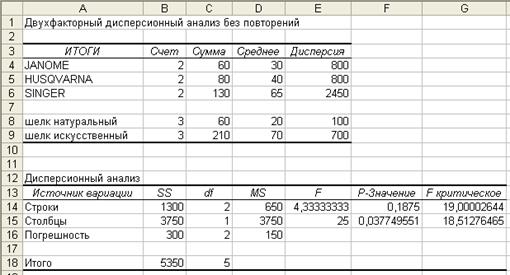
Рис. 8. Результат Двухфакторного

дисперсионного анализа без  повторений

Вывод. Вычисленное значение -критерия фактора  (тип станка) =4,3333 не попадает в критическую область , образованную правосторонним интервалом, поэтому гипотеза : принимается, т. е. считается, что влияние типа изготавливающего станка на качество пряжи не подтвердилось. Для -значения имеет место неравенство 0,1875>0,1, что говорит о хорошем согласии гипотезы  с выборочными данными.