Выборка и ее анализ. Точечные и интервальные оценки. Проверка статистических гипотез о параметрах нормально распределенной генеральной совокупности, страница 26

В статистике изучаются наблюденные данные случайных величин, поэтому стохастическая зависимость называется статистической или корреляционной.

Задачами корреляционного анализа являются:

- измерение степени связи;

- отбор факторов, оказывающих наибольшее влияние на результативный признак на основании степени связности между признаками;

- обнаружение неизвестных причинных связей.

Для оценки тесноты и вида связи между случайными величинами используются показатели ковариации и корреляции.

Пусть , , …,  выборка из генеральной совокупности двумерной случайной величиной , описывающей случайный эксперимент.

Выборочной ковариацией  называется среднее произведений отклонений значений выборок  и  от их средних , :

.

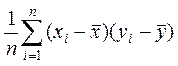Ковариация характеризует рассеивание значений выборок  и , а также линейную связь между ними.

Выборочной ковариационной матрицей называется матрица вида

.

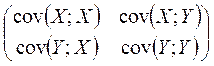Очевидно, что =, =.

Выборочная ковариационная матрица устанавливает взаимосвязь между выборками  и  из генеральных совокупностей значений случайных величин  и  по величине:

– при  большим значениям выборки  соответствуют большие значения выборки ;

– при  большим значениям выборки  соответствуют меньшие значения выборки  (или наоборот);

– при  данные выборок  и  не связаны.

Выборочным коэффициентом корреляции  случайных величин  и , между которыми предполагается линейная корреляционная связь, называется величина, определяемая по формуле

.

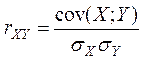Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таблица 1) [7].

Таблица 1. Шкала Чеддока

Теснота связи	Значение коэффициента корреляции при наличии
	прямой связи	обратной связи
Слабая	0,1–0,3	(-0,1)–(-0,3)
Умеренная	0,3–0,5	(-0,3)–(-0,5)
Заметная	0,5–0,7	(-0,5)–(-0,7)
Высокая	0,7–0,9	(-0,7)–(-0,9)
Весьма высокая	0,9–0,99	(-0,9)–(-0,99)

Выборочной корреляционной матрицей называется матрица вида

.

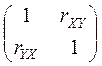Выборочная корреляционная матрица также устанавливает взаимосвязь наборов выборочных данных по величине:

1)     при  большим значениям выборки  соответствуют большие значения выборки ;

2)     при  большим значениям выборки  соответствуют меньшие значения выборки  (или наоборот);

3)     при  данные двух диапазонов некоррелированы;

4)     при  существует линейная функциональная зависимость между выборочными значениями  и .

Для нахождения выборочного коэффициентакорреляции используются формулы

,

.

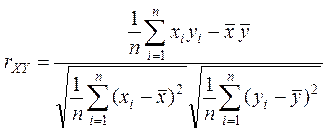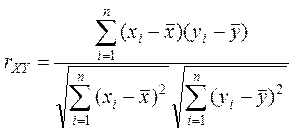При исследовании связи между несколькими случайными величинами находятся выборочные коэффициенты ковариации и корреляции между парами всех исследуемых величин и строятся соответствующие ковариационные и корреляционные матрицы. Например, ковариационная матрица для трех выборок , ,  имеет вид:

.

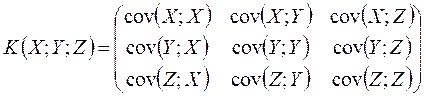Работа в Excel. Для нахождения ковариационной матрицы используется режим Ковариация из Анализа данных меню Сервис (Приложение 2). Результат анализа представлен в виде таблицы. Формулы и функции Excel, по которым рассчитываются соответствующие числовые характеристики, приводятся в таблице 2.

Таблица 2. Ковариационная матрица

	Столбец 1	Столбец 2
Столбец 1	КОВАР
Столбец 2	КОВАР	КОВАР

Для нахождения корреляционной матрицы используется режим Корреляция из Анализа данных меню Сервис (Приложение 2). Результат анализа представлен в виде таблицы. Формулы и функции Excel, по которым рассчитываются соответствующие числовые характеристики, приводятся в таблице 3.

Таблица 3. Корреляционная матрица

	Столбец 1	Столбец 2
Столбец 1	=1 КОРРЕЛ
Столбец 2	КОРРЕЛ	=1 КОРРЕЛ