а – схема для определения ЕЭ; б – схема для определения RЭ
Ток в сопротивлении R2 на этой схеме отсутствует, поэтому 
. Ток в
контуре R, E, R1 равен
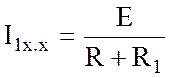
и напряжение холостого хода, а соответственно и эквивалентная ЭДС
.
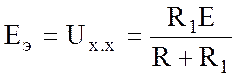Эквивалентное сопротивление RЭ находится по схеме рис. 2.9,б. Зажимы а и в при этом считаются входными:
.
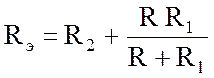В итоге ток IН, определяемый по эквивалентной схеме (рис. 2.8,б):
.
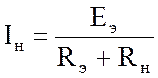Метод эквивалентного источника не относится к числу основных методов анализа электрических цепей. В ряде случаев он удобен, когда интерес представляет только один из токов в цепи или при физическом моделировании электрических цепей, когда требуется реализовать модель с минимальным количеством элементов.
2.5. Баланс мощностей
На основании закона сохранения энергии мощность, потребляемая в электрической цепи, должна быть равна мощности, поставляемой источниками. В состав потребляемой мощности входит мощность, рассеиваемая в сопротивлениях, а также мощность источников, находящихся в режиме потребителей.
Уравнение баланса мощностей имеет вид:
или 
.
В левой части равенства записана алгебраическая сумма произведений ЭДС источников на токи, протекающие через эти источники, и произведений токов источников тока на напряжения на их зажимах.
В правой части уравнения баланса мощностей записана арифметическая сумма произведений сопротивлений на квадраты токов, протекающих по этим сопротивлениям.
Примеры для определения знаков слагаемых приведены на рис.2.10.
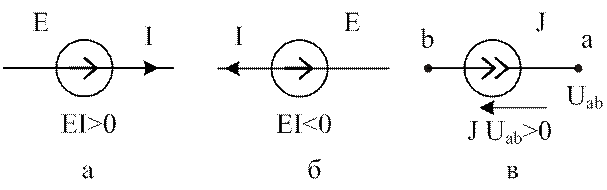
Рис.2.10. Примеры для определения знаков мощностей источников.
2.6. Преобразования электрических цепей
Преобразования электрических схем осуществляются с целью их упрощения. Примерами простейших преобразований является замена одним эквивалентным сопротивлением последовательного, параллельного и последовательно-параллельного соединений. Применяется еще и ряд более сложных преобразований, среди которых отметим эквивалентные преобразования соединений звездой и треугольником, а также преобразовании параллельного соединения ветвей с источниками ЭДС.
2.6.1. Эквивалентные преобразования соединений звездой и
треугольником
Указанные соединения представлены на рис. 2.11.
Эквивалентность соединений звездой и треугольником понимается в следующем смысле: при переходе от одной схемы к другой режим цепи, в составе которой находятся звезда и треугольник, не должен измениться. Это возможно, если напряжения U12, U23, U31 и токи I1, I2, I3 при переходе не изменяются. Следствием сохранения значений токов и напряжений является неизменность входных сопротивлений относительно одноименных пар зажимов преобразуемых участков.
Приравнивая соответствующие сопротивления, можно получить систему уравнений, решение которой приводит к необходимым соотношениям.
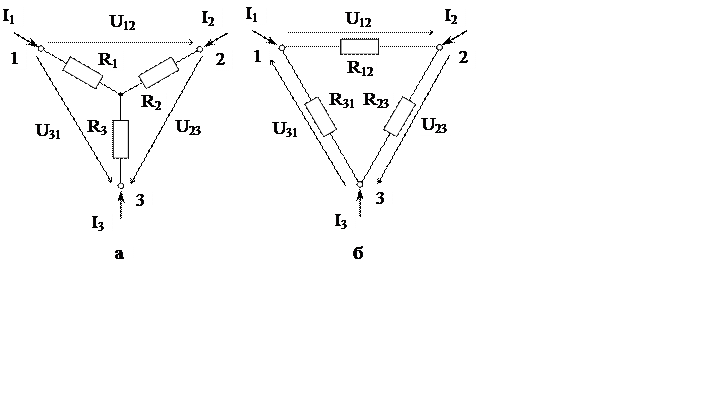
Рис.2.11. Эквивалентные схемы: а – соединение сопротивлений звездой;
б – соединение сопротивлений треугольником.
Между парами зажимов на левой схеме сопротивления соединены последовательно. На правой схеме между парами зажимов имеют место смешанное соединение сопротивлений. С учетом этого:
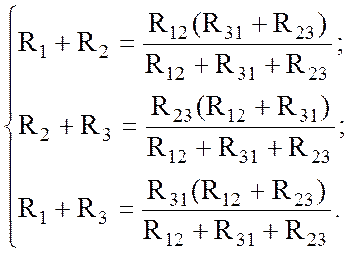(2.6)
Получили систему нелинейных алгебраических уравнений. Решение ее относительно R1, R2, R3 приводит к формулам перехода от треугольника к звезде. Если, наоборот, определять R12, R23, R31, то получим формулы перехода от звезды к треугольнику.
Используем следующий прием: из первого уравнения вычитаем второе и прибавляем третье. Получаем
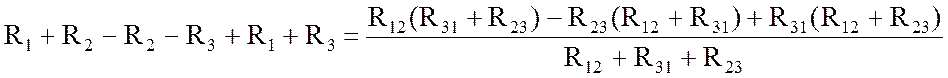
или
.
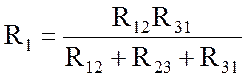Из полученной формулы легко устанавливается структура и закономерность расположения индексов в числителе, поэтому окончательный результат:
; 
; 
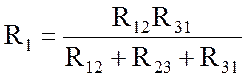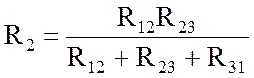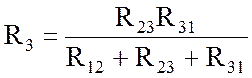. (2.7)
В (2.7) знаменатели формул одинаковы, а числители в правых частях содержат дважды индексы левых частей. Совпадение индексов означает, что произведения в числителях формул формируются ветвями, соединенными с данным узлом. Такое понимание облегчает составление формул (2.7) при произвольном обозначении сопротивлении ветвей.
Без решения системы (2.6) записываем формулы для преобразования соединения звездой в соединение треугольником:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.