Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 24

Делим  на сопротивления параллельных ветвей и находим все токи:

   

   

   

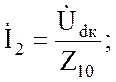
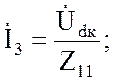
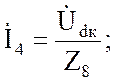
Мгновенные значения этих токов записываются аналогично току i₁.

По первому закону Кирхгофа для узла d или к.

         

Таким образом, первый закон Кирхгофа выполняется. Следующей проверкой правильности расчета токов ветвей является составление баланса мощностей.

3.  Баланс мощностей.

Комплексная мощность

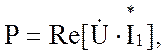
где  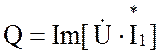 - соответственно действительная и мнимая части произведения комплекса приложенного к цепи напряжения на сопряженный комплекс входного тока

 

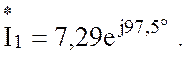
Активная и реактивная мощности, доставляемые источником в цепь, соответственно равны

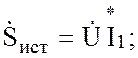
откуда

  

Найдем активную и реактивную мощности, потребленные приемниками (сопротивлениями) заданной цепи:

Расхождение составляет:

         

       

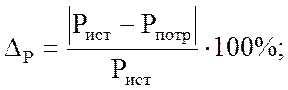
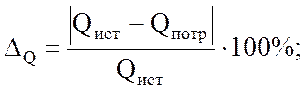
4.  Построение топографической векторной диаграммы.

Обычно строят лучевую диаграмму токов, векторы которых исходят из начала координат, и топографическую диаграмму напряжений.

При построении топографической диаграммы напряжений учитывают фазовый сдвиг между вектором тока, протекающего через элемент электрической цепи (сопротивление, индуктивность, емкость), и вектором падения напряжения на нем. На сопротивлении эти векторы совпадают по направлению. На индуктивности вектор напряжения опережает вектор тока на угол 90⁰, на емкости – отстает на этот угол.

Построение топографической диаграммы начинается от точки а (см. рис.3.18), в направлении обхода по часовой стрелке.

Для выбора масштаба рассчитываются падения напряжения на всех элементах схемы:

                   

       

       

        

      

        

      

      

Удобными для построения данной векторной диаграммы являются следующие масштабы токов и напряжений:

  

Из начала координат проводим векторы     (рис.3.21). Помещаем точку  а  в начало координат. Потенциал точки b  отличается от потенциала точки  а  на величину падения напряжения в сопротивлении . По направлению вектора тока  откладываем из точки а в масштабе вектор этого напряжения, равный 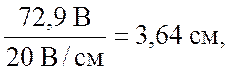  и получаем точку b.

Потенциал  отличается от  на величину . Вектор напряжения на емкости отстает по фазе от вектора тока на 90⁰. Поворачивая вектор тока по часовой стрелке на 90⁰ относительно точки b , получаем направление вектора . От точки b откладываем этот вектор и получаем точку  с. Вектор напряжения  опережает вектор тока на 90⁰. Поворачиваем вектор тока относительно точки  с  против часовой стрелки на 90⁰, от точки с откладываем вектор напряжения  и ставим точку d.

Точку k получают тремя путями – двигаясь от точки d  к точке k по ветвям. Рассмотрим один из путей. Из точки d проводим вектор напряжения  по направлению вектора тока  и получаем точку e. Поворачиваем вектор этого тока относительно точки e по часовой стрелке на 90⁰, откладываем вектор напряжения  и находим местоположение точки  k. Аналогично строим векторы падений напряжения  и

Рис 3.21. Диаграмма токов и напряжений

Соединяем точки  a и k, получаем вектор , изображающий в масштабе приложенное к заданной цепи напряжение. Убеждаемся, что модуль его U равен 190 В, а фаза составляет –70⁰ относительно положительной полуоси  +1, что соответствует исходным данным задачи и является еще одной проверкой правильности ее решения.

3.9. Задачи для самостоятельного решения

Условие задачи. Вэлектрической цепи (см. рис.3.22) с входным напряжением  определить комплексное действующее значение  входного тока при следующих параметрах:

      

            

         

      

Ответы приведены в табл.3.2.

Т а б л и ц а 3.2

Ответы к задаче на расчет цепи синусоидального тока

Номер варианта	Входной ток
	I,  А	α, 0
0	6,567	-22,1
1	12,598	-91,4
2	37,017	25,9
3	4,971	-14,7
4	3,284	-111,7
5	6,997	-60,8
6	12,861	-85,0
7	0,215	48,8
8	10,004	-23,5
9	2,314	37,2