Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 7

1.  Выбираются направления токов ветвей. Число токов равно числу ветвей схемы. Токи ветвей с источниками тока известны (см. п. 2.7.1, рис.2.13).

2.  Записываются уравнения по первому закону Кирхгофа. Их число на единицу меньше числа узлов схемы.

3.  Выбираются независимые контуры и направления их обхода.

4.  Записываются уравнения по второму закону Кирхгофа для независимых контуров, при этом уравнения для контуров, включающих источники тока, не составляются. Независимым считается такой контур, который от любого соседнего отличается хотя бы одной ветвью.

5.  В результате совместного решения уравнений, составленных по первому и второму законам Кирхгофа, определяются токи ветвей.

2.2.  Метод контурных токов

В этом методе за неизвестные принимают токи независимых контуров (контурные токи), а токи ветвей выражают через контурные.

Рассмотрим правила формирования уравнений на примере схемы, приведенной на рис. 2.3, в которой известны ЭДС и ток источника тока, а также все сопротивления.

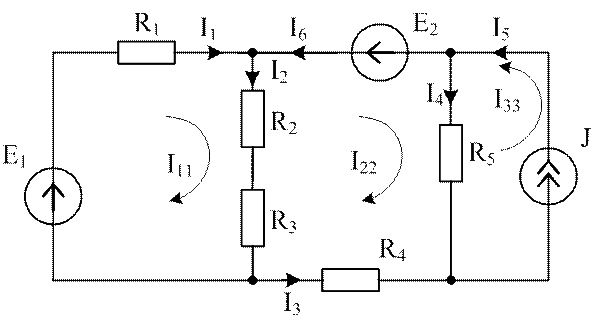
Рис. 2.3. Схема электрической цепи с контурными токами

Сначала выбираются независимые контуры и направления их обхода. Допустим, что в каждом контуре протекает свой контурный ток, совпадающий с направлением обхода – I₁₁, I₂₂, I₃₃. Выберем направления токов ветвей и составим уравнения по второму закону Кирхгофа для выбранных контуров (для контура с источником тока уравнение не составляется, так как ):

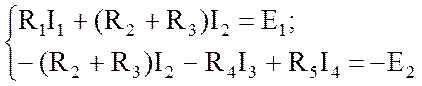                                (2.1)

Выразим токи ветвей через контурные

;  ;  ;  ;  ;  ; 

и подставим в систему (2.1):

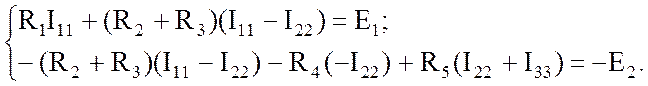
После группировки получим:

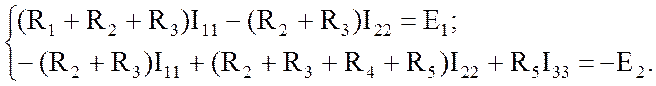
В конечном итоге получим систему уравнений:

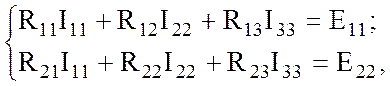                              (2.2)

где R₁₁, R₂₂ – собственные сопротивления контуров 1 и 2, каждое из которых равно сумме сопротивлений, входящих в данный контур;

R₁₂ = R₂₁, R₁₃, R₂₃ – общие или взаимные сопротивления контуров. Общее сопротивление равно сопротивлению ветви, общей для рассматриваемых контуров. Общие сопротивления берутся со знаком «плюс», если контурные токи в них направлены одинаково и со знаком «минус», если контурные токи направлены встречно. Если контуры не имеют общей ветви, то их общее сопротивление равно нулю. В рассматриваемом примере R₁₃ = 0;

Е₁₁, Е₂₂ – контурные ЭДС, каждая из которых равна алгебраической сумме ЭДС данного контура. ЭДС берется со знаком «плюс», если ее направление совпадает с направлением контурного тока, если не совпадает – со знаком «минус».

Структура уравнений (2.2), использующая понятия собственных и взаимных сопротивлений контуров, а также контурных ЭДС, является общей для метода контурных токов. В зависимости от сложности исследуемой цепи изменяется лишь количество уравнений.

2.2.1.  Последовательность определения токов ветвей методом

контурных токов

1.  Выбираются независимые контуры и направления контурных токов.

2.  Записывается система уравнений в общем виде. Число уравнений равно числу независимых контуров схемы минус число контуров, содержащих источники тока. Количество слагаемых в левой части уравнения равно числу независимых контуров.

3.  Определяются коэффициенты при неизвестных – собственные и общие сопротивления контуров, а также контурные ЭДС. Если общей ветвью контуров является источник ЭДС без сопротивления, то общее сопротивление этих контуров равно нулю.

4.  Рассчитываются контурные токи.

5.  Выбираются направления токов ветвей.

6.  Определяются токи ветвей.

2.3.  Метод узловых потенциалов

В этом методе за неизвестные принимают потенциалы узлов схемы.

Рассмотрим правила формирования уравнений на примере схемы, приведенной на рис. 2.4, в которой известны ЭДС и ток источника тока, а также все сопротивления.

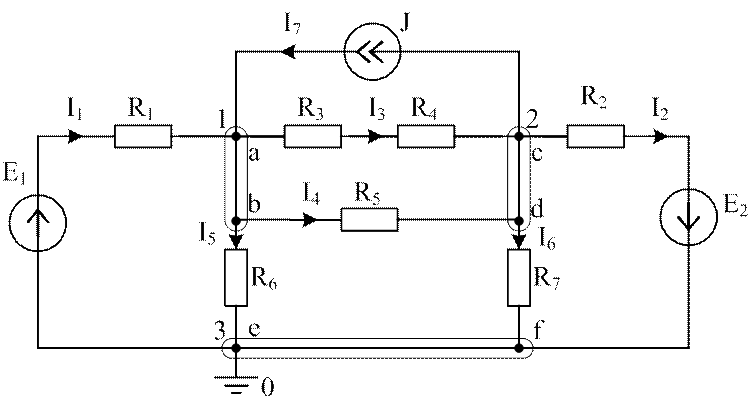
Рис. 2.4. Электрическая схема для метода узловых потенциалов

В этой схеме два неизвестных потенциала  и , поскольку , , , потенциал одного из узлов, в данном случае , принимается равным нулю, что на схеме обозначают заземлением узла 3 ().