В данном случае токи параллельных ветвей ![]() и
и ![]() не
находятся в противофазе, а потому не могут компенсировать друг друга. Резонанс
токов здесь обусловливается равенством между емкостным током
не
находятся в противофазе, а потому не могут компенсировать друг друга. Резонанс
токов здесь обусловливается равенством между емкостным током ![]() и
реактивной составляющей
и
реактивной составляющей ![]() тока
тока ![]() . В результате также выполняется основное условие наличия
резонанса – совпадение по фазе входного тока схемы I0 и приложенного напряжения U.
. В результате также выполняется основное условие наличия
резонанса – совпадение по фазе входного тока схемы I0 и приложенного напряжения U.
Числовые параметры схемы выбраны так, что из равенства
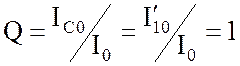 следует, что цепь не является высокодобротной.
следует, что цепь не является высокодобротной.
4.3.2. Резонанс в цепях с произвольным количеством
реактивных элементов
С возрастанием числа индуктивных и емкостных элементов в схемах резко увеличивается объем математических преобразований и вычислений, поэтому в качестве объекта для изучения возьмем схему с тремя реактивными элементами, изображенную на рис.4.12.
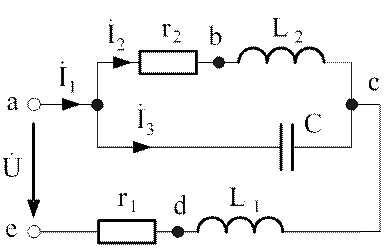
Рис.4.12. Схема с тремя реактивными элементами
Исследование явления резонанса в цепях, содержащих три и более реактивных элемента, имеет ту же основу, т.е. при резонансе входное сопротивление (проводимость) цепи становится чисто активным. Задача чаще всего сводится к определению резонансных частот и построению, если в том есть необходимость, частотных зависимостей реактивных сопротивлений (проводимостей) от частоты.
Входное комплексное сопротивление имеет вид:
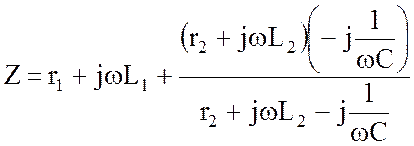 . (4.23)
. (4.23)
После разделения действительной и мнимой частей Z приходим к выражению:
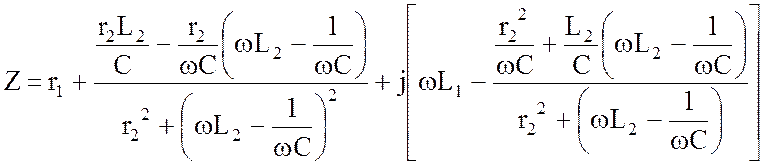 .(4.24)
.(4.24)
Далее используется только мнимая часть. Приравнивая ее
к нулю и подставляя ![]() , получаем уравнение
, получаем уравнение
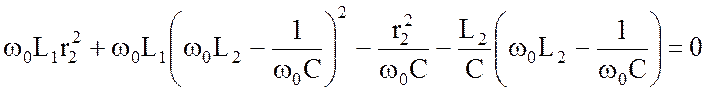 , (4.25)
, (4.25)
корни которого определяют резонансные частоты.
Положительный ответ на вопрос о возможности возникновения того или иного резонанса как уже указывалось, дают только положительные действительные корни уравнения (4.25). Любые другие типы корней (отрицательные действительные, комплексные или мнимые) указывают на отсутствие резонанса в рассматриваемой схеме.
Например, при численных значениях параметров схемы (рис.4.12) – r1 = 23 Ом, L1 = 0,274 Гн, r2 = 35 Ом, L2 = 0,340 Гн, C = 20 мкФ - уравнение (4.25) приобретает вид:
![]() .
.
Его корни имеют следующие значения:
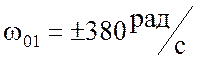 ;
; 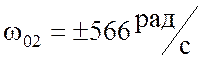 .
.
Из полученных корней два действительные, положительные, следовательно, можно сделать вывод о том, что в схеме наблюдаются резонансы при двух значениях частот:
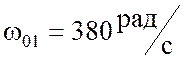 и
и 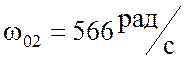 .
.
Чтобы ответить на вопрос о типе того или иного
резонанса, необходимо дополнительно провести расчет режимов схемы при
полученных резонансных частотах. На рис.4.13 и 4.14 представлены результаты
расчета токов и векторные диаграммы, построенные в одном масштабе для схемы
рис.4.12 при входном напряжении U = 2В на частотах 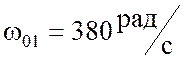 и
и 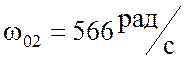 .
.
При численных значениях параметров схемы рис.4.12 – r1 = 23 Ом, L1 = 0,274 Гн, r2 = 35 Ом, L2 = 0,340 Гн, C = 1000 мкФ - уравнение (4.25) приобретает вид:
![]()
и его корни:
![]() ,
, ![]() .
.
что говорит о наличии одной резонансной частоты.
Удобство использования комплексного сопротивления или проводимости определяется топологией схемы, а решение уравнений x = 0 или b = 0 приводит к одинаковым результатам.
Результаты расчета:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Резонанс токов при частоте ![]() с-1 обусловлен токами параллельных ветвей I2 и I3. Но, как
и ранее, эти токи не находятся в противофазе, поэтому полностью компенсируются
реактивные составляющие этих токов
с-1 обусловлен токами параллельных ветвей I2 и I3. Но, как
и ранее, эти токи не находятся в противофазе, поэтому полностью компенсируются
реактивные составляющие этих токов ![]() и
и ![]() ,
которые относительно входного напряжения U сдвинуты на 900.
Составляющая
,
которые относительно входного напряжения U сдвинуты на 900.
Составляющая ![]() отстает от U на
900, а
отстает от U на
900, а ![]() – опережает, поскольку первая обусловлена индуктивностью,
а вторая – емкостью.
– опережает, поскольку первая обусловлена индуктивностью,
а вторая – емкостью.
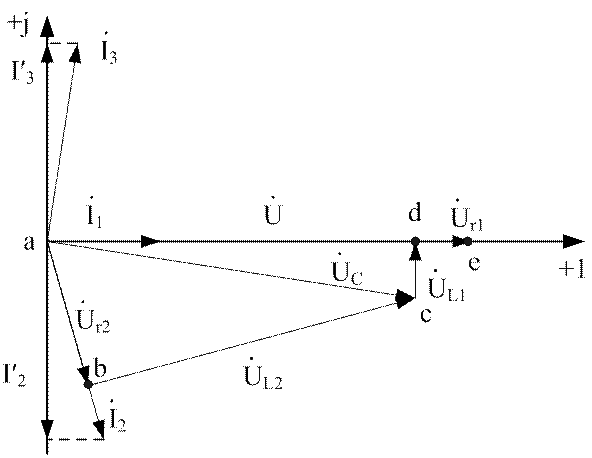
Рис.4.13. Диаграммы токов и напряжений при ![]() (резонанс токов)
(резонанс токов)
В режиме резонанса реактивные токи превышают по величине входной ток схемы:
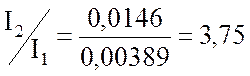 ,
, 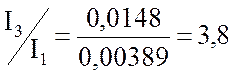 ,
,
следовательно,
добротность цепи при частоте ![]() с-1
можно оценивать значением
с-1
можно оценивать значением ![]() .
.
Результаты расчета: ![]() В;
В; 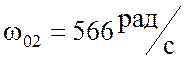
![]() ;
; ![]() А;
А; ![]() А.
А.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.