Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 28

После подстановки и вычислений определяем комплексное действующее значение входного тока цепи

А.

Соответствующая векторная топографическая диаграмма приведена на рис.3.30.

Пояснения к диаграмме.

Напряжение между точками 1 и 2 схемы соответствует разности напряжений, созданных во второй катушке явлениями само- и взаимоиндукции, т.е.

По аналогии

Кроме того

;   ;   ;  .

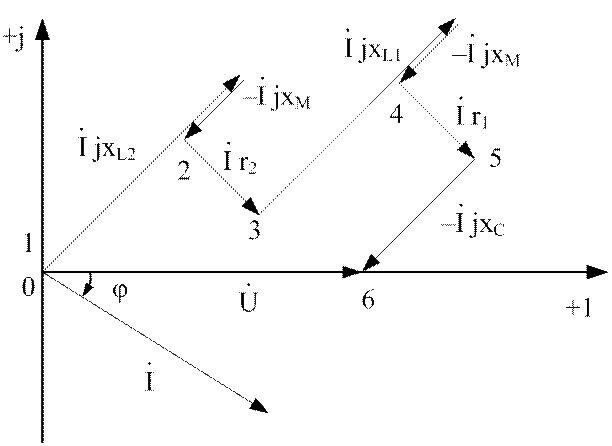
Рис.3.30. Диаграмма напряжений

Пример 2. К первичной обмотке трансформатора без стального сердечника (рис.3.31) подведено напряжение  = 120 В. Параметры схемы:

,  ,       ,  ,          ,     ,         .

Требуется:

а) определить напряжение на нагрузке ;

б) построить векторную диаграмму напряжений в каждом контуре схемы.

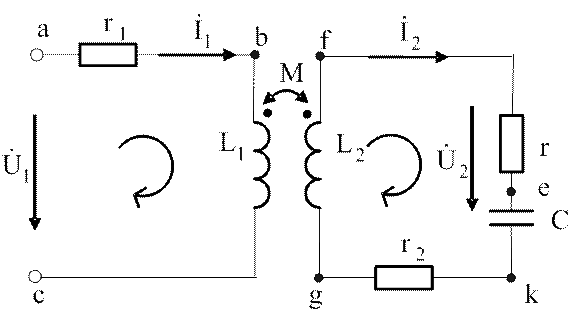
Рис. 3.31. Схема трансформатора

Решение.

Напряжение  на нагрузке rC можно вычислить, предварительно определив токи  и . С этой целью составим два уравнения по второму закону Кирхгофа, направив обходы контуров по токам.

Сравнивая направления токов относительно одноименных зажимов, делаем вывод, что включение катушек встречное, поэтому падения напряжения взаимной индукции отрицательные:

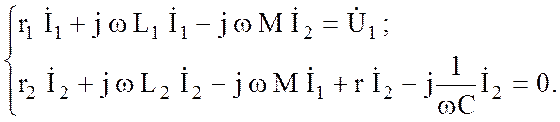
Упростим эти выражения, обозначив собственные сопротивления контуров  Z₁  и Z₂, взаимное сопротивление Z_М:

;

;

.

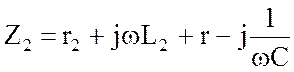Тогда система уравнений:

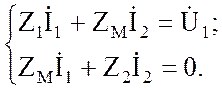
После подстановки и расчетов получаем:

;                       ;

;                  .

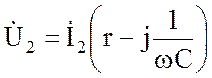Построение векторной диаграммы (рис.3.32) начинаем с векторов токов  и . Затем из начала координат по направлению вектора  откладываем в масштабе вектор падения напряжения  и под углом  – вектор . Поскольку включение катушек встречное, то вектор  падения напряжения в катушке  от тока  отстает от вектора этого тока на угол 90⁰. Суммирующим является вектор входного напряжения . Аналогично строится векторная диаграмма падений напряжений во втором контуре, где вектор  отстает на 90⁰ от вектора тока . Сумма векторов равна нулю.

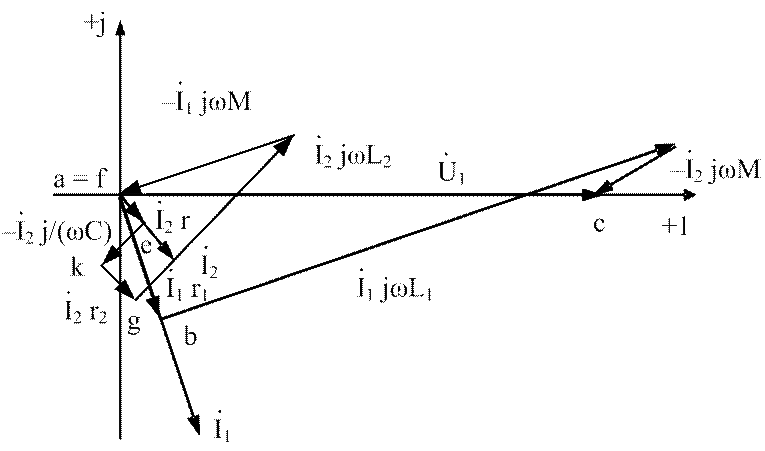
Рис. 3.32. Диаграмма напряжений

4.  РЕЗОНАНСНЫЕ  ЯВЛЕНИЯ  В  ЭЛЕКТРИЧЕСКИХ  ЦЕПЯХ

Резонансные явления могут возникать в электрических цепях, содержащих индуктивности и емкости. Резонанс в цепи с последовательным соединением индуктивности и емкости называют резонансом напряжений или последовательным резонансом. При параллельном соединении тех же элементов может возникать резонанс токов.

В сложной разветвленной цепи могут иметь место оба вида резонанса.

4.1.  Резонанс напряжений

Наиболее ярко особенности этого явления проявляются в цепи с последовательным соединением элементов r, L и С (см. рис.3.11,а).

Входное комплексное сопротивление этой схемы:

,                 (4.1)

где .

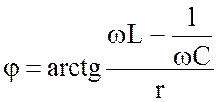Изменяя частоту, индуктивность или емкость, можно добиться равенства нулю реактивного сопротивления в составе (4.1).

Будем считать, что варьируемым параметром является угловая частота . Изменяя частоту при неизменных значениях индуктивности и емкости, придем к условию

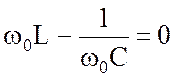      ,                                        (4.2)

которое рассматривается как условие резонанса.

Угловая частота

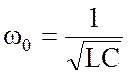                                                      (4.3)

называется резонансной.

При резонансе напряжений, как следует из (4.1), входное сопротивление становится чисто активным:

.                                                    (4.4)

Это значение является минимальным, поэтому ток I в схеме становится максимальным.

Кроме того, из (4.1) также следует, что угол  = 0 и входной ток цепи совпадает по фазе с напряжением.

Совпадение по фазе входного напряжения и тока является основным признаком наличия резонанса не только в рассматриваемом контуре, но и в любой другой цепи.

Напряжения  и  при последовательном соединении элементов L и С находятся в противофазе, т.е. сдвинуты одно относительно другого на 180⁰. Если  их амплитуды и действующие значения неодинаковы. При выполнении условия резонанса  амплитуды становятся одинаковыми. Отсюда и название резонанс напряжений.