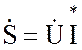Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 23

         или 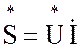                                           (3.65)

Чаще используется первая форма записи.

Пусть ; ; .

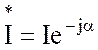Осуществим подстановку этих значений в (3.65):

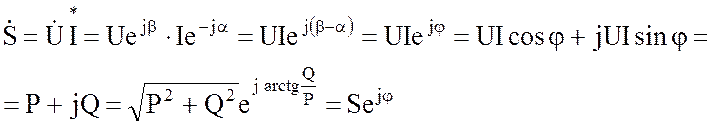 (3.66)

Интересное свойство комплексной мощности, как видно из (3.66) выразилось в возможности объединить в одном выражении все установленные ранее понятия мощности: S = UI – полную мощность,  – активную мощность,  – реактивную мощность. Поэтому комплексная мощность широко используется в расчетах.

Важное значение в энергетике имеет параметр, который называется коэффициентом мощности. Это есть отношение активной мощности к полной:

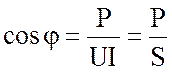.                                                   (3.67)

Косвенно этот параметр характеризует соотношение между активной мощностью и реактивной. Предельное его значение  = 1 достигается при отсутствии реактивных элементов. В идеальной реактивной цепи  = 0. В реальных условиях желательны режимы с максимальными экономически обоснованными значениями . Низкие значения коэффициента мощности показывают, что высока доля реактивной мощности. Такие режимы нежелательны, так как требуют повышенных значений токов в линиях для нежелательного двухстороннего обмена частью реактивной энергии между источником и приемниками электроэнергии. Повышенные токи обусловливают повышенные потери в линиях.

Широко используется параметр, который непосредственно характеризует соотношение между активной и реактивной мощностями:

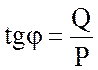.                                                    (3.68)

3.7.5. Баланс мощностей

Исходным моментом в составлении или проверке баланса мощностей является равенство комплексных мощностей, отдаваемых источником и потребляемых электрической цепью. При одном источнике:

                                              (3.69)

или

откуда следуют равенства

;           .

Мощности P_ист и Q_ист определяются, как правило, через входное напряжение и входной ток анализируемой схемы:

;       .                 (3.70)

С использованием выражения для комплексной мощности

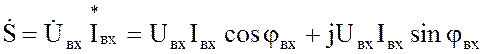   .                   (3.71)

Составляющие P_ист и Q_ист удобно записывать поэлементно:

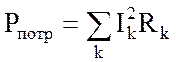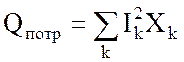;     .                        (3.72)

При этом следует учитывать, что все составляющие активной мощности  положительны. Слагаемые  имеют разные знаки. При использовании формы записи комплексной мощности (3.71) индуктивные составляющие  должны иметь знак плюс, а емкостные составляющие  – минус.

3.8. Пример расчета разветвленной цепи синусоидального тока

Электрическая цепь (рис.3.18) с входным напряжением  характеризуется следующими параметрами:

                            

                         

                                      

      

Определить комплексное входное сопротивление, комплексные и мгновенные значения токов, проверить баланс мощностей, построить топографическую векторную диаграмму.

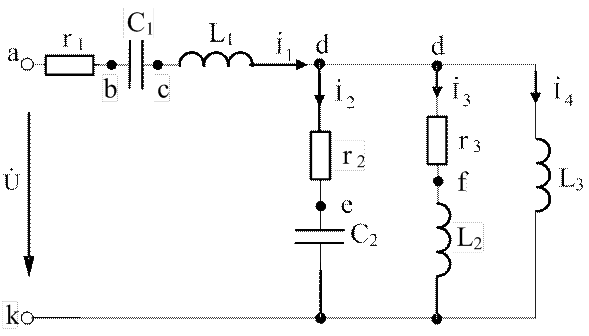
Рис.3.18. Расчетная схема

Решение.

Угловая частота ; с^-1, тогда приложенное напряжение , а действующее в комплексной форме В.

1.  Определение комплексного входного сопротивления цепи (рис.3.19).

Найдем комплексы всех сопротивлений цепи:

   ;

;

 

       

        

          

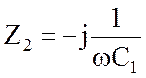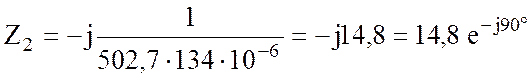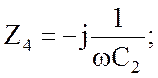
Сложим последовательно соединенные сопротивления:

      

      

Полученную схему (рис.3.19) преобразуем в одноконтурную (рис.3.20)

                 

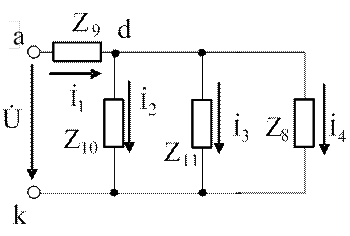
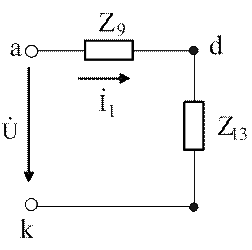
Рис.3.19. Схема с комплексными           Рис. 3.20. Одноконтурная

                                      сопротивлениями                                                схема

   

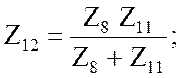
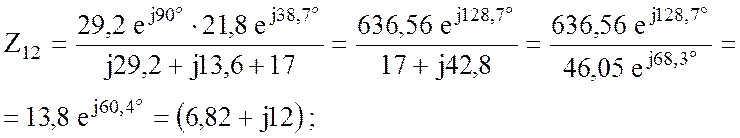
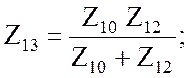
В результате комплексное входное сопротивление заданной цепи

2.  Расчет токов ветвей.

По закону Ома входной ток

    

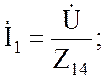
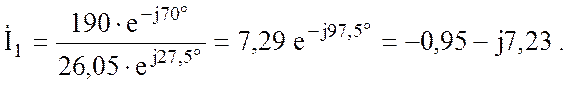
Мгновенное значение входного тока

Чтобы найти токи , , , необходимо определить напряжения на зажимах ветвей, по которым протекают эти токи. Поскольку все эти три ветви подключены к одной и той же паре узлов а и с (см. рис.3.18), то напряжения будут одинаковыми и равными . По закону Ома это напряжение (см. рис.3.18)