Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 6

В цепях постоянного тока напряжения на элементах цепи и токи - постоянные величины. Вследствие этого напряжение на индуктивности и ток в емкости приобретают нулевые значения, что следует из формул (1.9) и (1.12), в силу равенства нулю соответствующих производных:

;                  .

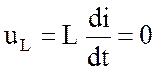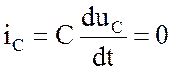Поэтому индуктивность не оказывает сопротивления постоянному току, а емкость, наоборот, воспринимается как бесконечное сопротивление, т.е. разрыв соответствующего участка цепи. Вследствие этого, при математическом исследовании в качестве пассивных элементов используются сопротивление R и обратная ему величина проводимость 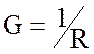. В качестве активных элементов выступают источник ЭДС и источник тока. Взаимная индуктивность М в данном случае также себя не проявляет, несмотря на то, что физически магнитные связи присутствуют.

Цепи синусоидального тока характеризуются полным набором элементов R, L, C и М. Присутствие или отсутствие того или иного из указанных элементов зависит от конкретной схемы.

2.  РАСЧЕТ  ЭЛЕКТРИЧЕСКИХ  ЦЕПЕЙ  ПОСТОЯННОГО  ТОКА

Постоянные токи обусловлены действием источников постоянных напряжений (ЭДС) и источников постоянных токов. Используемые при анализе основные физические величины – ЭДС, напряжения, токи и потенциалы имеют обозначения: Е, U, I, .

Основой для построения различных алгоритмов или способов расчета электрических цепей являются первый и второй законы Кирхгофа. Многие частные задачи также решаются с использованием преобразований цепей, упрощающих их топологию.

Преимущественно решаются задачи анализа электрических цепей. Суть их состоит в следующем: заданы активные и пассивные параметры электрической цепи, требуется определить токи ветвей и другие представляющие интерес физические величины, зависящие от этих токов.

Существуют еще задачи синтеза электрических цепей, когда требуется по заданным функциям цепей определять топологию и параметры цепей. Эти задачи являются более сложными и в настоящем пособии не рассматриваются.

2.1.  Законы Кирхгофа

Первый закон Кирхгофа формулируется для узла электрической цепи: алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю. При этом подходящие к узлу токи записываются с одним знаком, отходящие – с другим.

Например, для узла, изображенного на рис.2.1, можно записать

или

.

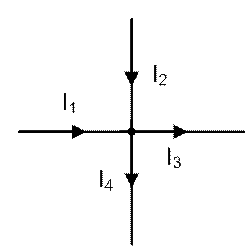
Рис 2.1. Узел электрической схемы

В первом случае с плюсом записаны токи, подходящие к узлу, во втором – плюс имеют отходящие токи.

Второй закон Кирхгофа формулируется для контура электрической цепи: алгебраическая сумма падений напряжений на участках контура равна алгебраической сумме ЭДС того же контура. При этом, если направление ЭДС совпадает с направлением обхода контура, то она берется со знаком «плюс», если не совпадает – со знаком «минус». Падение напряжения на элементе берется со знаком «плюс», если направление тока в элементе совпадает с направлением обхода, если не совпадает – со знаком «минус».

Например, для контура, показанного на рис. 2.2, можно записать:

.

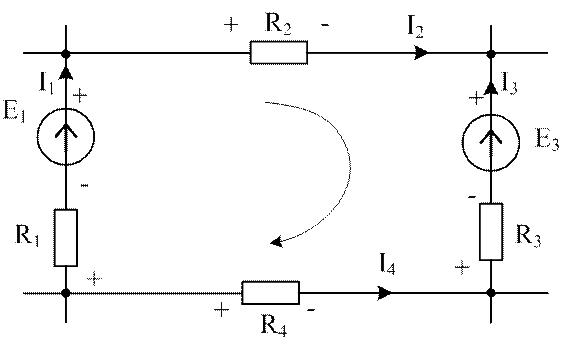
Рис. 2.2. Контур электрической схемы

Физическое содержание приведенного соотношения состоит в следующем.

Как известно, электрический ток в металлах связан с направленным движением электронов. В электротехнике направление тока выбрано противоположным, т.е. представляется как направление перемещения положительных зарядов. Положительные заряды перемещаются от точек с большими потенциалами к точкам, имеющим более низкий потенциал. Именно такая ситуация отражена на схеме рис. 2.2 знаками плюс и минус.

В сопротивлениях R₁ и R₂ обход совершается от плюса к минусу, т.е. потенциал в направлении обхода снижается и имеет место падения напряжения R₁I₁ и R₂I₂, входящие в левую часть уравнения со знаком плюс.

Сопротивления R₃ и R₄, наоборот повышают потенциал в направлении обхода контура, поэтому в уравнение произведения R₃I₃ и R₄I₄ включены со знаком минус.

2.1.1. Последовательность определения токов ветвей по законам

Кирхгофа