Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 30

Ширина полосы пропускания определяется точками пересечения резонансных кривых с прямой, соответствующей значению тока 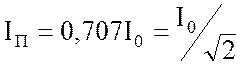. При данном значении тока мощность, теряемая в сопротивлении r равна половине потерь мощности при резонансе: .

На рис.4.3 первой кривой соответствует узкая полоса пропускания . У второй кривой полоса пропускания  значительно шире.

Поэтому закономерен следующий вывод: чем выше добротность, тем уже полоса пропускания.

Есть еще понятие избирательности резонансного контура как фильтра. Чем уже полоса пропускания, тем выше избирательность фильтра. Следовательно, значение добротности непосредственно, определяет качество фильтра по отмеченному критерию – способности выделять полезный сигнал, в данном случае ток, в более узком диапазоне частот.

Наконец, легко показать, что в диапазоне частот от нулевой до резонансной рассматриваемая схема имеет активно-емкостной характер, а при частотах, превышающих резонансную частоту  – активно-индуктивный. Так при частоте  емкостное сопротивление равно 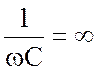. Ток в схеме при этом равен нулю, напряжение источника приложено только к емкости и угол сдвига фаз . При увеличении частоты до значения  значение  стремится к нулю. При дальнейшем увеличении частоты знак угла    изменяется на положительный и в пределе при  становится чисто индуктивным, т.е. . Следовательно резонансная частота  является точкой раздела между отрицательными и положительными значениями угла сдвига фаз. В диапазоне частот  напряжение по фазе отстает от тока при  наоборот, напряжение опережает ток.

4.2.  Резонанс токов

Особенности резонанса токов (параллельного резонанса) удобно рассматривать на примере схемы рис.3.12 с параллельным соединением элементов r, L, C.

Входная комплексная проводимость этой схемы

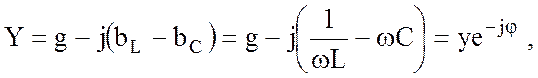                (4.7)

где ;

.

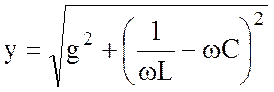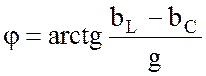При резонансной частоте  реактивная проводимость принимает нулевое значение

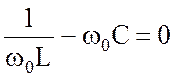,                                              (4.8)

откуда резонансная частота

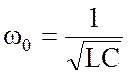  .                                                  (4.9)

На векторной диаграмме (см. рис.4.4) ток I_L отстает от напряжения на 90⁰, а ток I_C опережает напряжение на 90⁰. Действующие значения этих токов равны, поэтому их сумма равна нулю.

Входной ток схемы I, равен току ветви с активным сопротивлением I_r. Угол сдвига фаз    равен нулю. В итоге входной ток цепи по фазе совпадает с входным напряжением и выполняется сформулированное в предыдущем разделе условие резонанса.

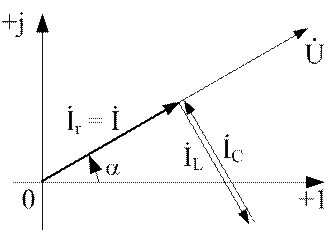
Рис. 4.4. Резонанс токов

Проводимость 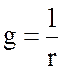 есть минимальное значение входной проводимости. Поэтому при резонансе токов входной ток схемы, в отличие от резонанса напряжений, принимает минимальное значение:

.                                                  (4.10)

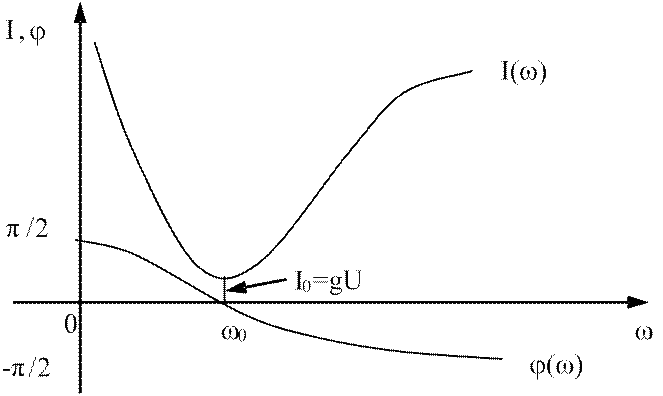
Рис.4.4. Частотные характеристики при резонансе токов

При нулевой частоте  сопротивление индуктивной ветви схемы рис.3.12 равно нулю (). Поэтому весь ток проходит только по этой ветви, имеет индуктивный характер и теоретически бесконечен. Вследствие этого левая ветвь кривой  на рис.4.5 начинается в бесконечности, а начало кривой угла сдвига фаз соответствует значению 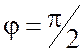. В режиме резонанса ток имеет минимальное значение, а угол сдвига фаз равен нулю. В области изменения частоты от нуля до  схема на входных зажимах воспринимается как активно-индуктивная. При частотах  преобладает ток емкостной ветви, поэтому схема воспринимается как активно-емкостная.

Рассмотрим далее значения реактивных проводимостей при резонансной частоте :

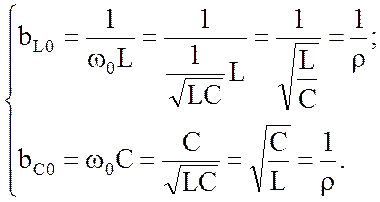                              (4.11)

Добротность в данном случае определяется как отношение реактивных проводимостей к активной:

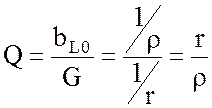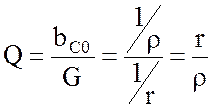;                     .                   (4.12)

В итоге получили формулу добротности

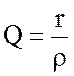,                                                   (4.13)

которая выглядит как обратная по отношению к аналогичной формуле для последовательной цепи.