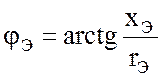Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 21

  – угол сдвига фаз между входным напряжением  u  и входным током  i₁.

Реактивное сопротивление x_Э может быть как положительным (индуктивным), так и отрицательным (емкостным). Это зависит от соотношения параметров рассматриваемой схемы.

Комплексное действующее значение входного тока определяется после этого как

.

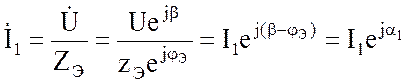По комплексу тока  в случае необходимости записывается мгновенное значение тока

.

Множитель  обозначает переход от действующего значения тока I₁ к амплитудному значению , поскольку в окончательном виде должно быть записано выражение

.

К значениям токов ветвей можно прийти разными путями, по наиболее общий  путь характеризуется следующими этапами:

Выражаем напряжение  :

.

Это напряжение приложено к обеим параллельным ветвям, поэтому

;               .

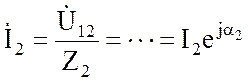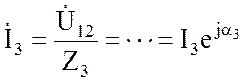По полученным значениям комплексов токов записываются мгновенные значения

;   .

В процессе вычислений приходится применять преобразование комплексных чисел, так как для операции сложения и вычитания необходима алгебраическая форма комплексных чисел, а умножение и деление более удобно осуществлять, используя показательную или экспоненциальную форму.

3.7. Мощности

В области цепей синусоидального тока используется несколько понятий мощности: мгновенная мощность, активная мощность, реактивная, полная и мощность в комплексной форме или комплексная  мощность.

3.7.1. Мгновенная мощность

Представляет собой произведение мгновенных значений напряжения и тока

р = u i.                                                     (3.54)

Пусть ,  т.е. ток отстает от напряжения на угол сдвига фаз  . Подстановка этих значений в (3.54) дает

.

Произведение синусов преобразуется в соответствии с выражением

.

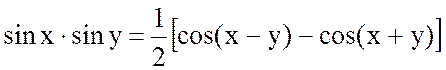Полагая,    приходим к результату

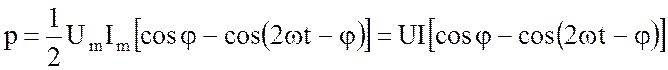.                                                                                          (3.55)

Как видно из (3.55), мгновенная мощность является периодической функцией, изменяющейся с двойной частотой по отношению к частоте напряжения и тока.

Рассмотрим сначала функцию мгновенной мощности для сопротивления  к (см. рис.3.15,а).

Периодическая функция мгновенной мощности в этом случае не имеет отрицательных значений. Ее среднее значение согласно (3.55) равно произведению действующих значений напряжения и тока , поскольку

Мгновенная мощность пульсирует с двойной частотой, но нигде не меняет знака, что указывает на однонаправленность потока электрической энергии от источника к сопротивлению. Возврат энергии источнику отсутствует. Поэтому в качестве главного свойства и отмечается необратимость процесса преобразования энергии в сопротивлении r.

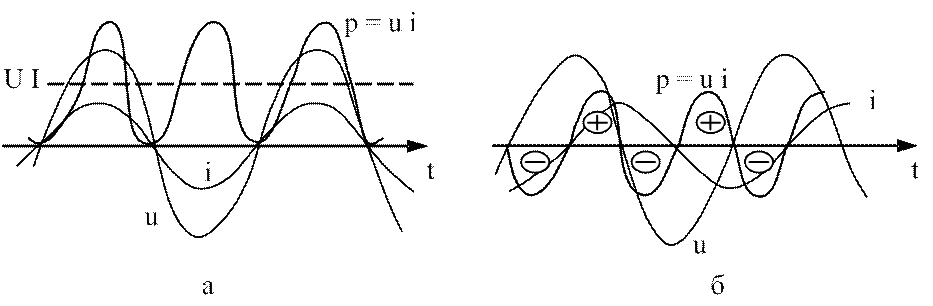
Рис.3.15. Мгновенная мощность:

а – сопротивление r; б – индуктивность L

В индуктивности  L  угол сдвига фаз  , поэтому в (3.55)   и кривая мгновенной мощности симметрична относительно оси времени (см.рис.3.15,б). Это значит, что в части периода энергия поступает от источника в индуктивность, в другой – возвращается источнику. Там где «плюс», энергия магнитного поля индуктивности увеличивается до какого-то максимального значения, в пределах площадок со знаком «минус» - она уменьшается до нуля.

В идеальной цепи процесс энергетического обмена между источником, например, ЭДС и индуктивностью не сопровождается потерями. Также ведет себя и идеальная цепь с емкостью, только здесь энергетические процессы связаны с энергией электрического поля.

В реальных условиях любые электромагнитные процессы сопровождаются потерями или затратами электроэнергии. На рис.3.16 в качестве иллюстрации приведен график мгновенной мощности для цепи, содержащей сопротивление и индуктивность.

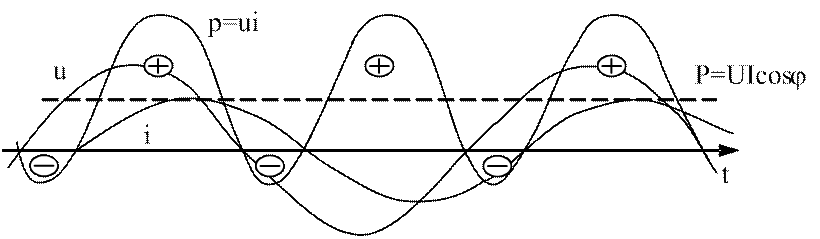
Рис.3.16. Мгновенная мощность цепи с r и L

Особенность рис.3.16 в том, что кривая мгновенной мощности несимметрична относительно оси времени. Отрицательные площадки меньше положительных, т.е. возвращается источнику энергии меньше, чем он отдает в электрическую цепь. Отмеченная разница определяется необратимым потреблением энергии в цепи, которое выражает среднее значение мгновенной мощности, обозначенное как .