Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 18

Это означает, что при математическом исследовании электрической цепи синусоидального тока можно операции с синусоидальными функциями заменить операциями с комплексными числами (комплексными амплитудами).

Соотношения (3.27) определяют аналогичные (3.28) соответствия для производной и интеграла:

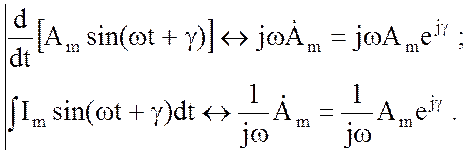                                   (3.29)

В целом формируется так называемое линейное преобразование, в котором основную роль играют операции с комплексными числами.

При расчете электрических цепей используются комплексные амплитуды напряжений, токов, ЭДС и других представляющих интерес величин. При этом имеют место следующие соответствия:

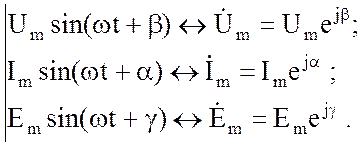                                                        (3.30)

Для иллюстрации особенностей использования комплексных соотношений обратимся к схемам рис.3.7.

Для активно-индуктивной цепи (рис.3.7,а) справедливо уравнение (3.17):

.

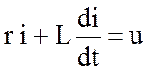В соответствии с (3.29) и (3.30) представим это уравнение в комплексной форме, используя понятие комплексных амплитуд:

 .                                        (3.31)

Преобразуем (3.31):

или

   .                                                  (3.32)

где  – сопротивление цепи в комплексной форме или просто комплексное сопротивление. Это сопротивление записывается также и в показательной или экспоненциальной форме:

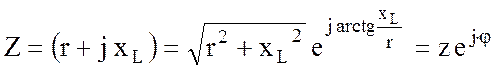,                                 (3.33)

где 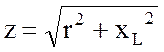 – есть установленное ранее полное сопротивление. Следовательно, полное сопротивление z является модулем комплексного сопротивления z;  – угол сдвига фаз между напряжением и током.

Появилась также величина

,                                                 (3.34)

которая называется индуктивным сопротивлением в комплексной форме.

Итогом решения является комплексная амплитуда тока

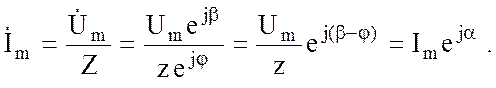                  (3.35)

По комплексной амплитуде тока легко записывается мгновенное значение тока:

.

В случае цепи r, C (см. рис.3.7,б) имеют силу соотношения:

;           ;

,

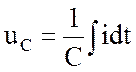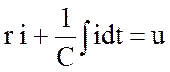на основе которых формируется уравнение для комплексных амплитуд:

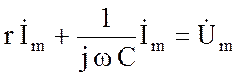,                                               (3.36)

преобразуемое в выражение

   ,                                                  (3.37)

где .

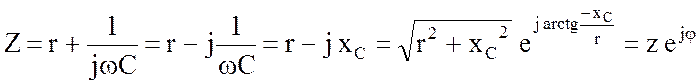Здесь снова 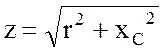 – полное сопротивление активно-емкостной цепи;

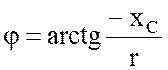 – угол сдвига фаз.

Комплексная амплитуда тока

 .

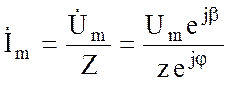Параметр 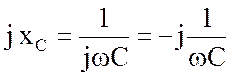 в данном случае представляет емкостное сопротивление в комплексной форме.

В операциях с комплексными числами полезно понимание следующих соотношений:

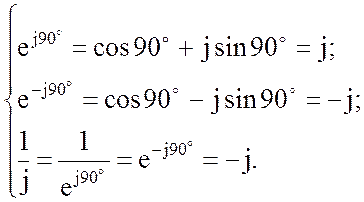                                                         (3.38)

Например, емкостное сопротивление было записано в двух формах

,

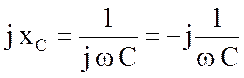т.е. использовалось вытекающее из (3.38) правило .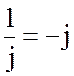

Равенство  показывает, что умножение комплекса на  j  определяет поворот соответствующего этому комплексному числу вектора на 90⁰ в положительном направлении, т.е. против часовой стрелки. Умножению на  наоборот, соответствует поворот вектора на 90⁰ по часовой стрелке.

3.4. Действующее значение синусоидального напряжения и тока

Математически действующее значение функции представляет собой среднеквадратичное значение

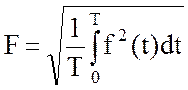.                                            (3.39)

Аналогично выражаются и действующие значения электрических величин

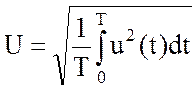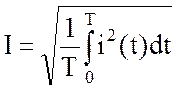;    ,                               (3.40)

где  u, i – мгновенные значения напряжения, тока;

 Т - период функции.

Пусть, например, напряжение представляется в виде  . Подстановка этой функции в (3.40) дает

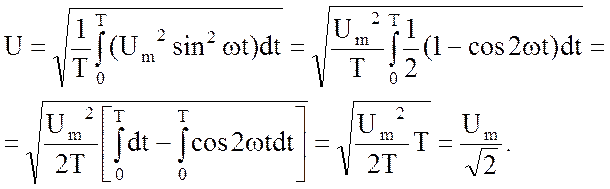                 (3.41)

Второй интеграл под корнем равен нулю как определенный интеграл от периодической функции на целом числе периодов.

В итоге действующее значение отличается от амплитудного в    раз.

Полученный результат справедлив для действующего значения любой физической величины, изменяющейся по синусоидальному закону:

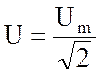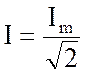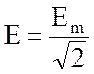;   ;         .                           (3.42)

Действующие значения электрических величин широко используются в электротехнике, поскольку тепловое действие тока, силы взаимодействия контуров с токами, электромагнитные моменты электрических машин и ряда силовых электромагнитных устройств переменного тока обусловлены именно действующими значениями токов.