Добротность характеризует соотношение между токами
индуктивной и емкостной ветвей и током через ветвь с сопротивлением r.
Если 
то реактивные
токи 
и 
при
резонансе меньше активного 
. Значение 
показывает кратность превышения реактивных токов по отношению к активному.
Схема рис.3.12 с параллельным соединением элементов r, L, C
обладает характеристиками так называемого заграждающего или режекторного
фильтра. В области частот, примыкающей к резонансной, входное сопротивление
цепи максимально. Поэтому ток минимален, откуда и название «заграждающий
фильтр». Добротность, как и в предыдущем случае влияет на форму кривой 
и другие
характеристики фильтра.
4.3. Резонанс в электрических цепях произвольной структуры
В практике используются более сложные схемы электрических фильтров и другие электрические цепи, содержащие различное количество реактивных элементов. В области электрических фильтров явление резонанса используется как полезное или необходимое явление. Но в других областях явление резонанса может возникать как нежелательное явление, приводящее к повышенным значениям напряжений или токов. При высоких добротностях электрических цепей, т.е. в цепях с малыми потерями в активных сопротивлениях, напряжения и токи в резонансных режимах могут достигать опасных значений. Поэтому понимание резонансных свойств той или иной электрической системы является важной задачей.
Во всех случаях в качестве критерия наличия резонансного режима выступает условие совпадения начальных фаз входных напряжения и тока исследуемой электрической цепи. С этим условием согласуется условие обращения в нуль реактивной составляющей входного комплексного сопротивления (проводимости) электрической цепи. Поэтому исходным этапом математического исследования резонансных свойств любой электрической цепи является выделение из состава комплексного входного сопротивления (проводимости) реактивной составляющей и приравнивание последней нулю.
В целом расчет проводится с реализацией следующих этапов.
1. Записывается входное сопротивление или входная проводимость цепи.
2. Входное сопротивление (проводимость) разделяется на действительную и мнимую части.
3. Выделяется реактивное сопротивление (проводимость) цепи (мнимая часть) и приравнивается к нулю.
4. Полученное уравнение решается относительно искомой неизвестной (частоты, индуктивности, емкости, сопротивления).
Как правило, первым этапом решения является вычисление резонансных частот, поскольку именно реализация этого этапа отвечает на вопрос возможны в данной цепи резонансы или нет.
В цепях с двумя реактивными элементами определяется и исследуется одна резонансная частота.
Для цепей с тремя реактивными элементами определяются и исследуются две резонансные частоты. Количество резонансных частот возрастает с увеличением числа реактивных элементов (индуктивных и емкостных).
4.3.1. Резонанс в цепях с двумя реактивными элементами
На рис.4.6 изображена группа схем, в которых индуктивность и емкость включены последовательно или находятся в составе последовательного соединения двухэлементных участков схем.
Схема рис.4.6,а уже исследована в разделе 4.1 и выявлены особенности, характеризующие резонанс напряжений. В остальных схемах также может возникать только резонанс напряжений в силу отмеченной их структуры. В качестве примера рассмотрим схему рис.4.6,б.
Входное сопротивление этой схемы:
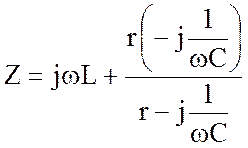. (4.14)
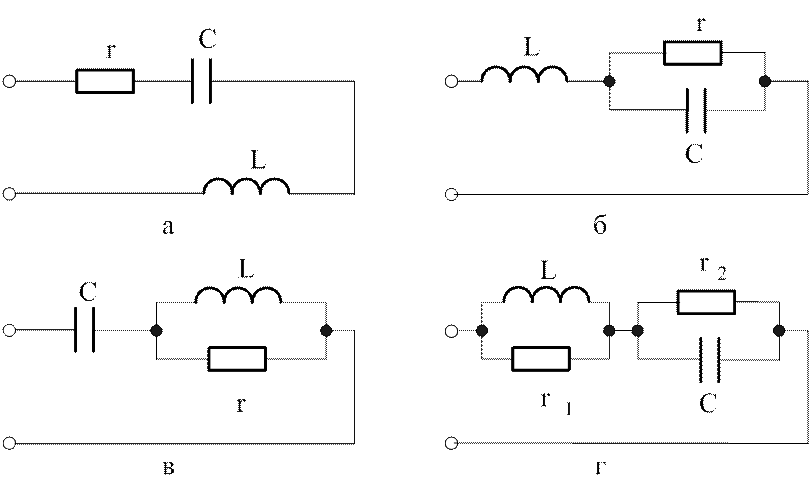
Рис. 4.6. Схемы, в которых возможен резонанс напряжений
Преобразуем полученное выражение, умножая числитель и знаменатель на сопряженный комплекс знаменателя:
.
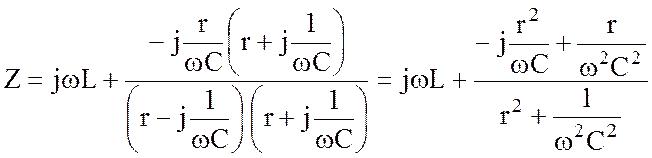Далее осуществляется разделение действительной и мнимой частей полученного выражения:
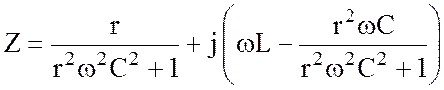(4.15)
и для определения резонансной частоты мнимая часть (4.15) приравнивается нулю:
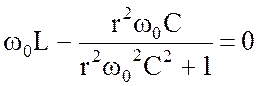. (4.16)
В итоге получается алгебраическое уравнение второй
степени относительно резонансной частоты 
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.