Основы теории цепей постоянного и переменного токов: Учебное пособие для самостоятельной работы студентов, страница 22

3.7.2. Активная мощность

Активная мощность определена как среднее значение мгновенной мощности:

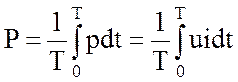.                                               (3.56)

Мгновенную мощность выражает формула (3.55). После подстановки (3.55) в (3.56) получаем:

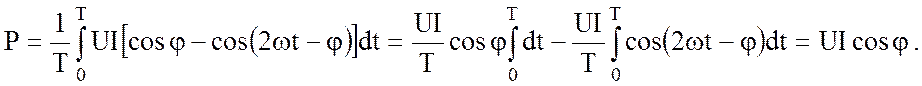                                                                                    (3.57)

Второй интеграл в приведенном выражении равен нулю, как определенный интеграл на целом числе периодов.

В итоге активная мощность в цепях синусоидального тока выражается формулой

,                                                   (3.58)

находящей широкое практическое использование.

Произведение

                                                                                (3.59)

есть полная мощность, поэтому активная мощность записывается также в виде

.                                                    (3.60)

Единица измерения активной мощности ватт (Вт); полная мощность измеряется в вольт-амперах (ВА).

Активная мощность включает в свой состав две составляющие: полезно потребляемую мощность, как, например, мощность на валу электродвигателя, а также мощность потерь в активных сопротивлениях элементов электрооборудования и линиях. Поэтому она характеризует необратимый однонаправленный поток электроэнергии от источника к нагрузкам или потребителям.

В активной цепи (см. рис.3.15,а) поток электроэнергии направлен только к потребителю, поэтому активная мощность равна полной мощности

,                                                     (3.61)

т.е. вся электроэнергия, отдаваемая потребителю, используется для совершения полезной работы с учетом потерь в сопротивлениях элементов.

В идеализированной реактивной цепи (см. рис.3.15,б), активная мощность равна нулю, так как необратимые процессы потребления и потерь энергии отсутствуют. Энергии магнитного или электрического полей периодически меняют свои значения от нулевого до максимального, подчиняясь соотношениям (1.10) и (1.13):

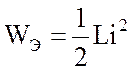 и .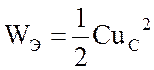

Наконец, в реальных условиях электрических цепей или систем с потерями активная мощность выступает как некая разность между мощностью, отдаваемой источником и мощностью, которую источник получает обратно.

3.7.3. Реактивная мощность

Понятие реактивной мощности не имеет такого же четкого определения как активная мощность. Можно лишь констатировать, что появление этого понятия применительно к электрическим цепям физически связано с поведением электрических и магнитных полей элементов электрических цепей и электромагнитных устройств.

Реактивная мощность определяется формулой

.                                                  (3.62)

Единица измерения реактивной мощности  Q – вольт-ампер реактивный (вар).

Ответить на вопрос, каковы истоки этой формулы, позволяют следующие рассуждения.

Полное сопротивление в цепи синусоидального тока выражается, как уже известно, формулой

.                                                  (3.63)

Этой формуле соответствует прямоугольный треугольник со сторонами z, r, x (см. рис.3.17,а), который называется треугольником сопротивлений.

Рис.3.17. Треугольник:

а – сопротивлений; б – мощностей

Умножим левую и правую часть (3.63) на  I²:

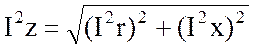
С учетом треугольника сопротивлений:

 – полная мощность;

 – активная мощность;

- реактивная мощность.

Поэтому справедлива запись

                                                              (3.64)

и появляется так называемый треугольник мощностей (см. рис.3.17,б).

В результате можно сделать вывод, что понятие реактивной мощности (3.62) в теорию электрических цепей введено по формальному признаку, а именно, реактивная мощность, как понятие, является составляющей треугольника мощности. По любому другому выражению для реактивной мощности  Q  построить треугольник мощностей было бы невозможно. 

3.7.4. Мощность в комплексной форме или комплексная  мощность

Комплексная мощность представляет собой произведение комплекса напряжения на сопряженный комплекс тока или, наоборот, сопряженный комплекс напряжения на комплекс тока: